2005 II 1
From QED
The energy density in the plasma is:
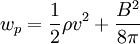
So the total energy in the plasma is:
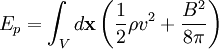
The ideal MHD equations with p = 0 give:
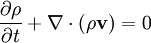
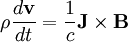
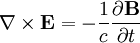
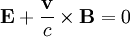
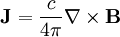
Combining:
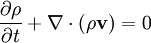
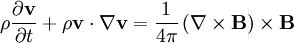
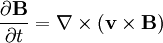
So:
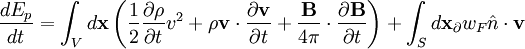
Plugging in:
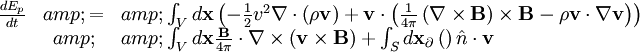
Rearranging:
![\begin{array}{rcl} \frac{dE_{p}}{dt} & = & \frac{1}{2}\int_{V}d\mathbf{x}\left(-v^{2}\nabla\cdot\left(\rho\mathbf{v}\right)-\rho\left(\mathbf{v}\cdot\nabla\right)v^{2}\right)\\ & & +\frac{1}{4\pi}\int_{V}d\mathbf{x}\left[-\left(\nabla\times\mathbf{B}\right)\cdot\left(\mathbf{v}\times\mathbf{B}\right)+\mathbf{B}\cdot\nabla\times\left(\mathbf{v}\times\mathbf{B}\right)\right]\\ & & +\int_{S}d\mathbf{x}_{\partial}\left(\frac{1}{2}\rho v^{2}+\frac{B^{2}}{8\pi}\right)\hat{n}\cdot\mathbf{v}\end{array}](../../../images/math/3/5/b/35b42529a39bbd92433d7674b780b70e.png)
Or, using vector identities 1, 7 and 9:
![\begin{array}{rcl} \frac{dE_{p}}{dt} & = & -\frac{1}{2}\int_{V}d\mathbf{x}\nabla\cdot\left(v^{2}\rho\mathbf{v}\right)\\ & & +\frac{1}{4\pi}\int_{V}d\mathbf{x}\nabla\cdot\left[\left(\mathbf{v}\times\mathbf{B}\right)\times\mathbf{B}\right]\\ & & +\int_{S}d\mathbf{x}_{\partial}\left(\frac{1}{2}\rho v^{2}+\frac{B^{2}}{8\pi}\right)\hat{n}\cdot\mathbf{v}\end{array}](../../../images/math/8/4/6/8469d69ce17c32375dde4e0b3bb220b7.png)
Then:
![\begin{array}{rcl} \frac{dE_{p}}{dt} & = & -\frac{1}{2}\int_{S}d\mathbf{x}_{\partial}v^{2}\rho\mathbf{v}\cdot\hat{n}\\ & & +\frac{1}{4\pi}\int_{S}d\mathbf{x}_{\partial}\left[\left(\mathbf{v}\times\mathbf{B}\right)\times\mathbf{B}\right]\cdot\hat{n}\\ & & +\int_{S}d\mathbf{x}_{\partial}\left(\frac{1}{2}\rho v^{2}+\frac{B^{2}}{8\pi}\right)\hat{n}\cdot\mathbf{v}\end{array}](../../../images/math/0/6/8/06833c857cf9d1b81cbd667b1c2d7e03.png)
Or:
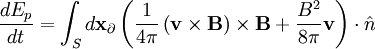
Expanding the double cross product:
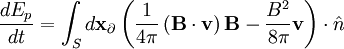
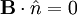 on the boundary:
on the boundary:
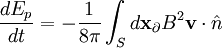
The vacuum energy density is:
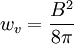
So:
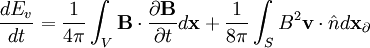
Plugging in for 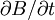 :
:
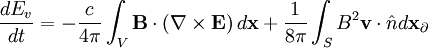
Using the vector identity:
![\frac{dE_{v}}{dt}=-\frac{c}{4\pi}\int_{V}\left[\nabla\times\left(\mathbf{E}\times\mathbf{B}\right)+\mathbf{E}\cdot\left(\nabla\times\mathbf{B}\right)\right]d\mathbf{x}+\frac{1}{8\pi}\int_{S}B^{2}\mathbf{v}\cdot\hat{n}d\mathbf{x}_{\partial}](../../../images/math/b/8/e/b8eafc965154cd90997258ca36f120ca.png)
Since 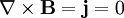 in the vacuum, and plugging
in
in the vacuum, and plugging
in 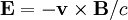 :
:
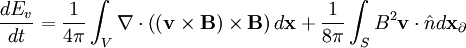
Expanding the double cross product, and changing the integral to a surface integral:
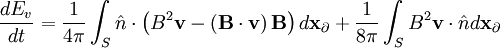
Since 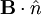 is zero on the surface:
is zero on the surface:
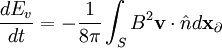
There will be no jump conditions at the plasma-vacuum interface, since there are no surface currents. The time derivative of the total energy will then be:
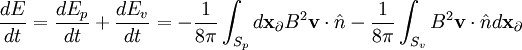
The vacuum boundary contains the plasma-vacuum boundary and the vacuum-container boundary:
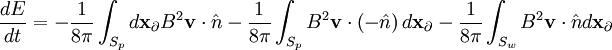
Where we have used the negative sign since the normal faces out of the vacuum, and so into the plasma. The total energy time derivative is then:
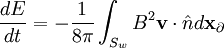
That is, the integral at the conducting wall of this quantity.
In MHD the E2 / 8π is considered small compared to the B2 / 8π term. Using Ohm's law:
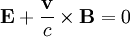
So:
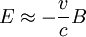
Then the electric field term over the magnetic field term gives:
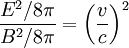
So since 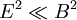 .
.
This page was recovered in October 2009 from the Plasmagicians page on Generals_2005_II_1 dated 20:25, 15 May 2007.












