2005 II 4
From QED
The wave equation is:
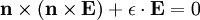
The two transverse waves have:
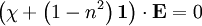
We can take the first two equations:
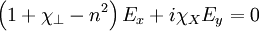
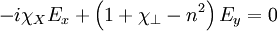
And combine them:
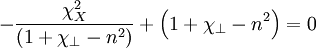
Expanding:
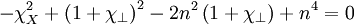
Which can be factored to:
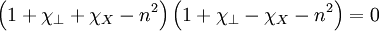
Giving dispersion relations:
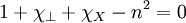
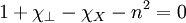
The last equation is longitudinal, so:
Or:
The term that goes to infinity at ω = ΩH is 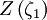 .
This term appears in the dispersion relation:
.
This term appears in the dispersion relation:
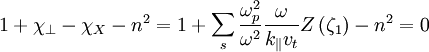
Using the dispersion relation:
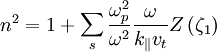
For ω real and very close to ΩH, 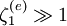 [note: this assumption comes from Stix, we assume it is based on <i>k</i><i>v</i><i>T</i><i>i</i>˜Ω<i>H</i>. This makes sense if it is reasonable to keep the ion term as <i>Z</i>(ζ), but is not necessarily true],
so we take the first term in the electron expansion:
[note: this assumption comes from Stix, we assume it is based on <i>k</i><i>v</i><i>T</i><i>i</i>˜Ω<i>H</i>. This makes sense if it is reasonable to keep the ion term as <i>Z</i>(ζ), but is not necessarily true],
so we take the first term in the electron expansion:
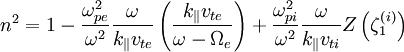
Since 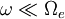 :
:
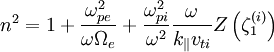
And by quasineutrality, 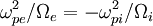 ,
so we will find:
,
so we will find:
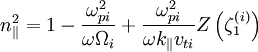
Because 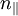 will not go
to infinity at the resonance.
will not go
to infinity at the resonance.
This page was recovered in October 2009 from the Plasmagicians page on Generals_2005_II_4 dated 20:35, 15 May 2007.












