2005 I 1
From QED
We consider the differential equation:
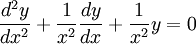
For 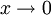 , the equation is singular, so we guess y˜eS:
, the equation is singular, so we guess y˜eS:
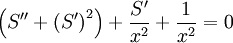
Balance between 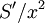 and
and 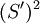 gives
gives 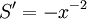 , which is dominant. There is an alternate
balance between
, which is dominant. There is an alternate
balance between 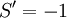 .
Finding the next term g for the first case:
.
Finding the next term g for the first case:
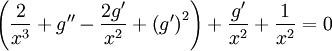
So balance between 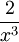 ,
, 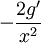 , and
, and 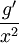 gives
gives 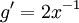 .
The other term is already less singular that lnx. The leading
asymptotic forms are then:
.
The other term is already less singular that lnx. The leading
asymptotic forms are then:
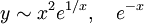
For 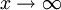 , the equation is again singular, so, guessing
y˜eS:
, the equation is again singular, so, guessing
y˜eS:
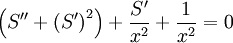
This time there is balance between 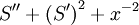 ,
giving
,
giving 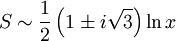 . So:
. So:
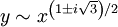
Or:
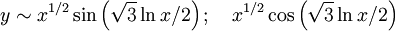
Warning- The below contains a sign error!
For 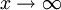 the equation is not singluar, so, writing
the equation is not singluar, so, writing
| y = | ∑ | anx − n − α |
| n |
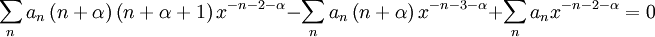
Shifting:
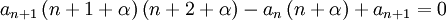
For n = 0, we want to find α s. t. the coefficient for an + 1 is zero:
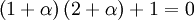
Or:
Which has solution:
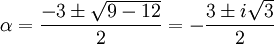
So we must have a0 = 0, but a1 is free. That term gives the leading asymptotic form for two solutions:
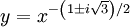
We know our solutions are real, so we can combine these solutions to be:
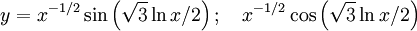
This page was recovered in October 2009 from the Plasmagicians page on Generals_2005_I_1 dated 20:20, 15 May 2007.












