Warning: jsMath requires JavaScript to process the mathematics on this page.
If your browser supports JavaScript, be sure it is enabled.

2005 I 4

From QED

< PlasmaWiki | Generals(Link to this page as [[PlasmaWiki/Generals/2005 I 4]])

Jump to: navigation, search

The canonical angular momentum is:

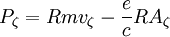
$P_{\zeta}=Rmv_{\zeta}-\frac{e}{c}RA_{\zeta}$

The flux may be defined as:

ψ = - R A ζ

So:

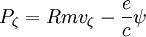
$P_{\zeta}=Rmv_{\zeta}-\frac{e}{c}\psi$

Taking the lagrangian derivative, the left side is zero since it is conserved:

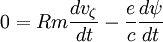
$0=Rm\frac{dv_{\zeta}}{dt}-\frac{e}{c}\frac{d\psi}{dt}$

Bounce averaging:

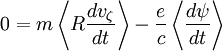
$0=m\left\langle R\frac{dv_{\zeta}}{dt}\right\rangle -\frac{e}{c}\left\langle \frac{d\psi}{dt}\right\rangle$

On average over a bounce, $R d v ζ / d t$ is zero, since it returns to the same position with the same velocity after one complete bounce. Therefore:

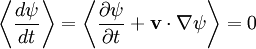
$\left\langle \frac{d\psi}{dt}\right\rangle =\left\langle \frac{\partial\psi}{\partial t}+\mathbf{v}\cdot\nabla\psi\right\rangle =0$

By Faraday's law:

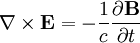
$\nabla\times\mathbf{E}=-\frac{1}{c}\frac{\partial\mathbf{B}}{\partial t}$

In terms of 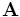$\mathbf{A}$ :

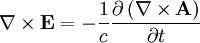
$\nabla\times\mathbf{E}=-\frac{1}{c}\frac{\partial\left(\nabla\times\mathbf{A}\right)}{\partial t}$

Interchanging derivatives:

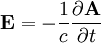
$\mathbf{E}=-\frac{1}{c}\frac{\partial\mathbf{A}}{\partial t}$

So:

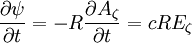
$\frac{\partial\psi}{\partial t}=-R\frac{\partial A_{\zeta}}{\partial t}=cRE_{\zeta}$

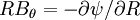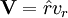Noting $RB_{\theta}=-\partial\psi/\partial R$ , and over a bounce average assuming $\mathbf{V}=\hat{r}v_{r}$ :

c R E ζ - v r R B θ = 0

So:

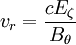
$v_{r}=\frac{cE_{\zeta}}{B_{\theta}}$

There is also diffusion, since there is a pressure gradient. We can estimate the banana diffusion by using a step size of $Λ i$ , and the ion-ion collision frequency, multiplying by $f T = ε 1 / 2$ , the fraction of trapped particles:

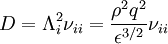
$D=\Lambda_{i}^{2}\nu_{ii}=\frac{\rho^{2}q^{2}}{\epsilon^{3/2}}\nu_{ii}$

The radial flux is then:

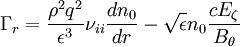
$\Gamma_{r}=\frac{\rho^{2}q^{2}}{\epsilon^{3}}\nu_{ii}\frac{dn_{0}}{dr}-\sqrt{\epsilon}n_{0}\frac{cE_{\zeta}}{B_{\theta}}$

The spitzer conductivity is modified to:

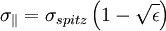
$\sigma_{\|}=\sigma_{spitz}\left(1-\sqrt{\epsilon}\right)$

because the trapped particles do not carry current. But the trapped particles do produce bootstrap current, due to the pressure gradient. The current is:

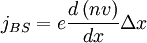
$j_{BS}=e\frac{d\left(nv\right)}{dx}\Delta x$

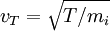$v_{T}=\sqrt{T/m_{i}}$ :

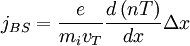
$j_{BS}=\frac{e}{m_{i}v_{T}}\frac{d\left(nT\right)}{dx}\Delta x$

Using $p = n T$ and $Δ x = Λ i = ρ i q / ε 1 / 2$ , the banana width:

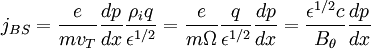
$j_{BS}=\frac{e}{mv_{T}}\frac{dp}{dx}\frac{\rho_{i}q}{\epsilon^{1/2}}=\frac{e}{m\Omega}\frac{q}{\epsilon^{1/2}}\frac{dp}{dx}=\frac{\epsilon^{1/2}c}{B_{\theta}}\frac{dp}{dx}$

The current density is then:

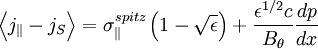
$\left\langle j_{\|}-j_{S}\right\rangle =\sigma_{\|}^{spitz}\left(1-\sqrt{\epsilon}\right)+\frac{\epsilon^{1/2}c}{B_{\theta}}\frac{dp}{dx}$

Onzager symmetry states that the cross terms in the flux-driving force matrix will be equal (symmetric about the diagonal). In this problem, it states that the coefficient of the 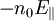$-n_{0}E_{\|}$ term in part a will be equal to the coefficient of the $- T e d n / d x$ term in part b.