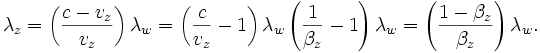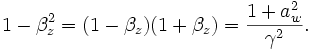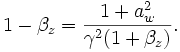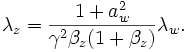2008 II 3
From QED
This problem asks us to consider the motion of a relativistic electron in a static magnetic field generated by a helical "wiggler" magnet configuration. This field is given by
where 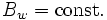 and
and 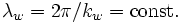 are the wiggler field amplitude and wavelength. The relativistic mass factor
are the wiggler field amplitude and wavelength. The relativistic mass factor 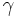 is given by
is given by
where 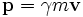 is the kinematic momentum.
is the kinematic momentum.
Part (a)
Solve for that particle velocities in the particle orbit (primed) frame using the relativistic Lorentz force equation, which in Gaussian units is given by
First, show that 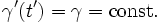 by taking its time derivative and applying the Lorentz force equation:
by taking its time derivative and applying the Lorentz force equation:
The notation in the above expression implicitly assumes that 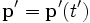 and
and 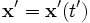 . The first term vanishes because
. The first term vanishes because 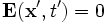 in this problem, and the second term vanishes due to orthogonality. This gives the result that
in this problem, and the second term vanishes due to orthogonality. This gives the result that 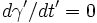 such that
such that
Now solve for the components of the particle orbit velocities in the primed frame. Use the method of characteristics to directly integrate both sides of the Lorentz force equation, which after inserting the wiggler magnetic field is given by
Because  is constant, it can be brought out through the time derivative, giving
is constant, it can be brought out through the time derivative, giving
Evaluating the cross product gives
which recombines into the Lorentz force equation giving
Separating the  and
and  components of the above equation gives
components of the above equation gives
and the 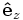 component gives
component gives
The goal is to express the right hand sides of the 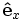 and
and 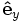 equations in terms of
equations in terms of 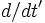 so that these equations can be directly integrated in
so that these equations can be directly integrated in 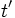 along the characteristics of the system. Noting that
along the characteristics of the system. Noting that
Substituting these expressions into the 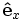 and
and 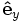 equations yields
equations yields
Directly integrating both sides with respect to 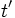 gives the final expressions for
gives the final expressions for 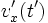 and
and 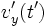 , which are
, which are
where 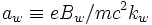 .
.
Going back to the equation for 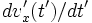 from the
from the 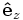 component of the Lorentz force equation, which is,
component of the Lorentz force equation, which is,
and substituting for 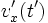 and
and 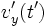 from above gives
from above gives
Thus, because 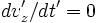 ,
, 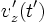 is simply
is simply
The above condition directly implies that
which is a quantity that is present in the expressions for 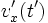 and
and 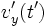 . Note: This last equation is already given in the problem.
. Note: This last equation is already given in the problem.
Part (b)
The spontaneous emission spectrum 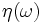 is given in the problem to be of the form
is given in the problem to be of the form
where 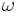 is the emission frequency,
is the emission frequency, 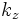 is the wavenumber,
is the wavenumber, 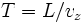 is the length of time that the electron is in the interaction region of length
is the length of time that the electron is in the interaction region of length 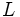 , and
, and 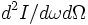 is the energy radiated per unit frequency interval per unit solid angle. The integration variable is
is the energy radiated per unit frequency interval per unit solid angle. The integration variable is 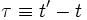 such that
such that 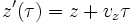 .
.
Defining 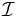 as the integral in the
as the integral in the 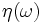 expression such that
expression such that
where the separated integrals 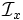 and
and 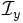 are given by
are given by
Exponentiating the 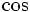 and
and 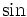 factors gives
factors gives
where
Substituting for 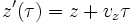 and combining terms gives
and combining terms gives
which can be directly integrated to give
This expression has resonant peaks near 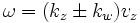 . The problem asks us to focus on the upshifted resonant peak near
. The problem asks us to focus on the upshifted resonant peak near 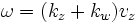 . Here,
. Here, 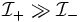 due to the resonant denominator, so only the
due to the resonant denominator, so only the 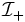 terms need to be considered when evaluating
terms need to be considered when evaluating 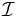 to find
to find 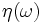 near the upshifted resonant peak. The reduced expressions for
near the upshifted resonant peak. The reduced expressions for 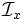 and
and 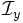 are now
are now
Defining
the expression for 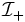 evaluates to
evaluates to
Factoring to find a 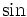 function gives
function gives
Now going back to evaluate 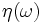 ,
,
Substituting for 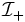 gives the final expression for
gives the final expression for 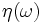 to be
to be
where ![\displaystyle\omega_{eff}\equiv[\omega - (k_z + k_w)v_z]/2](../../../images/math/8/7/8/878702e302f2bc51ce0adbb437a1479e.png) .
.
Part (c)
In this last part, we are asked to show that if the emitted radiation corresponds to light wave in vacuum such that 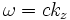 , then the radiation spectrum
, then the radiation spectrum 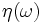 that we calculated above is maximized for a wavelength
that we calculated above is maximized for a wavelength 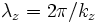 given by
given by
where 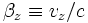 ,
, 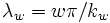 , and
, and 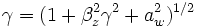 .
.
Because the final expression for 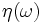 has a
has a 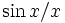 dependence, it will be maximized when
dependence, it will be maximized when 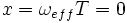 . Thus, examining
. Thus, examining
gives
From 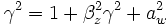 :
:
Thus
and, as desired,
![\mathbf{B}^0_w(\mathbf{x}) = -B_w\left[\cos(k_w z)\mathbf{\hat{e}}_x + \sin(k_w z)\mathbf{\hat{e}}_y\right],](../../../images/math/d/b/4/db4a500a6d469ea516dd3f84dbd88e4f.png)
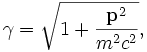
![\frac{d\mathbf{p}}{dt} = -e\left[\mathbf{E}(\mathbf{x},t) + \frac{\mathbf{p}\times\mathbf{B}(\mathbf{x},t)}{\gamma m c}\right].](../../../images/math/0/3/1/031bd14aeedcbfa24811e2cacde1e07e.png)
![\frac{d\gamma'(t')}{dt'} = \frac{d}{dt'}\left(\sqrt{1 + \frac{(\mathbf{p}')^2}{m^2 c^2}}\right) = \frac{1}{2\gamma'}\,\mathbf{p'}\cdot\frac{d\mathbf{p'}}{dt'}
= -\frac{e}{2\gamma'}\,\mathbf{p'}\cdot\left[\mathbf{E}(\mathbf{x}',t') + \frac{\mathbf{p'}\times\mathbf{B}(\mathbf{x}',t')}{\gamma' m c}\right]](../../../images/math/2/0/c/20c79bd68d112bccc7955379d4e2fd8f.png)
![\frac{d\mathbf{p}'}{dt'} = -e\left[\frac{\mathbf{p}\times\mathbf{B}^0_w(\mathbf{x}')}{\gamma' m c}\right]
= -\frac{e}{c}\left[\left(\frac{\mathbf{p'}}{\gamma'm}\right)\times\mathbf{B}^0_w(\mathbf{x}')\right]](../../../images/math/b/1/9/b196dfe3039658994bd0d2d44a100cdc.png)
![\frac{d\mathbf{p}'}{dt'} = \gamma m \frac{d\mathbf{v}'}{dt'}
= -\frac{e}{c}\left[\left(\frac{\mathbf{p'}}{\gamma'm}\right)\times\mathbf{B}^0_w(\mathbf{x}')\right]
= -\frac{e}{c}\bigg[\mathbf{v}'\times\mathbf{B}^0_w(\mathbf{x}')\bigg].](../../../images/math/7/1/8/7182fd8af72ecae3aeaf28ac1ae94e88.png)
![\mathbf{v}'\times\mathbf{B}^0_w(\mathbf{x}') = \mathbf{v}'\times\left[B^0_{w,x}(\mathbf{x}')\mathbf{\hat{e}}_x + B^0_{w,y}(\mathbf{x}')\mathbf{\hat{e}}_y\right]
= -v'_z B^0_{w,y}\mathbf{\hat{e}}_x + v'_z B^0_{w,x}\mathbf{\hat{e}}_y + \left(v'_x B^0_{w,y} - v'_y B^0_{w,x} \right)\mathbf{\hat{e}}_z,](../../../images/math/c/2/e/c2ea6e534cc1a348fb9a8ff049690ea0.png)
![\gamma m \frac{d\mathbf{v}'}{dt'} = -\frac{e}{c}\bigg[\mathbf{v}'\times\mathbf{B}^0_w(\mathbf{x}')\bigg]
= \frac{e}{c}\bigg[v'_z B^0_{w,y}\mathbf{\hat{e}}_x - v'_z B^0_{w,x}\mathbf{\hat{e}}_y - \left(v'_x B^0_{w,y} - v'_y B^0_{w,x} \right)\mathbf{\hat{e}}_z\bigg]](../../../images/math/2/8/3/283fb9ea3c5312c33a3d9bd8a1c4c77e.png)
![\displaystyle \gamma m \frac{dv'_x}{dt'} = \;\;\,\displaystyle\frac{e}{c}\,v_z'(t')B^0_{w,y}(\mathbf{x}')
= -\displaystyle\frac{e}{c}\,v_z'(t')B_w\sin[k_wz'(t')]](../../../images/math/9/6/4/9649d6de6fc771581b032befc3d05d0a.png)
![\displaystyle \gamma m \frac{dv'_y}{dt'} = -\displaystyle\frac{e}{c}\,v_z'(t')B^0_{w,x}(\mathbf{x}')
= \;\;\,\displaystyle\frac{e}{c}\,v_z'(t')B_w\cos[k_wz'(t')]](../../../images/math/4/5/d/45d98732210af090d7008babab4393eb.png)
![\gamma m \frac{dv'_z}{dt'} = \frac{e}{c}\bigg[v'_x(t') B^0_{w,y}(\mathbf{x}') - v'_y(t') B^0_{w,x}(\mathbf{x}')\bigg]
= -\frac{e}{c}\,B_w\bigg[v'_x(t')\sin[k_wz'(t')] - v'_y(t')\cos[k_wz'(t')]\bigg].](../../../images/math/2/8/2/282c253f78903f627ad9153bf73e76e7.png)
![\displaystyle \frac{d}{dt'}\cos[k_wz'(t')] = \displaystyle -k_w\left(\frac{dz'(t')}{dt'}\right)\sin[k_wz'(t')] = -k_w v'_z(t')\sin[k_wz'(t')]](../../../images/math/0/6/5/0653f49926a9ed77321db1221f3efee5.png)
![\displaystyle \frac{d}{dt'}\sin[k_wz'(t')] = \;\;\,\displaystyle k_w\left(\frac{dz'(t')}{dt'}\right)\cos[k_wz'(t')] = \;\;\,k_w v'_z(t')\cos[k_wz'(t')]](../../../images/math/5/5/2/55220e8e9d79cac132969e5ed56988d4.png)
![\displaystyle \gamma m \frac{dv'_x}{dt'} = -\displaystyle\frac{e}{c}\,v_z'(t')B_w\sin[k_wz'(t')] =
\displaystyle\left(\frac{eB_w}{c k_w}\right)\frac{d}{dt'}\cos[k_wz'(t')]](../../../images/math/9/4/8/9485b6a7ab19e7a11f27a39ef8abd755.png)
![\displaystyle \gamma m \frac{dv'_y}{dt'} = \;\;\,\displaystyle\frac{e}{c}\,v_z'(t')B_w\cos[k_wz'(t')] =
\displaystyle\left(\frac{eB_w}{c k_w}\right)\frac{d}{dt'}\sin[k_wz'(t')]](../../../images/math/0/2/9/029a3219f0ad39e764c9c3999b8dd565.png)
![v'_x(t') = \displaystyle\frac{ca_w}{\gamma}\cos[k_wz'(t')]](../../../images/math/6/7/3/673f0dba310ae34fd65f92a823076848.png)
![v'_y(t') = \displaystyle\frac{ca_w}{\gamma}\sin[k_wz'(t')]](../../../images/math/d/6/c/d6c8b830a9080a1d4c0c6e47bf065f83.png)
![\gamma m \frac{dv'_z}{dt'} = -\frac{e}{c}\,B_w\bigg[v'_x(t')\sin[k_wz'(t')] - v'_y(t')\cos[k_wz'(t')]\bigg],](../../../images/math/5/5/7/55718ba06298eea096b9f4fb3214a17f.png)
![\gamma m \frac{dv'_z}{dt'} = -\frac{ea_w}{\gamma}\,B_w\bigg[\cos[k_wz'(t')]\sin[k_wz'(t')] - \sin[k_wz'(t')]\cos[k_wz'(t')]\bigg] = 0](../../../images/math/3/5/5/3551b3b21a1c89d8378f7fb9635ff605.png)
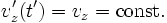
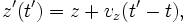
![\eta(\omega) \equiv \frac{1}{T}\frac{d^2I}{d\omega d\Omega} = \frac{e^2\omega^2}{4\pi^2c^3T}
\Bigg|\int_0^T\!d\tau\,\Big[v'_x(\tau)\mathbf{\hat{e}}_x + v'_y(\tau)\mathbf{\hat{e}}_y\Big]\exp\Big\{ik_z z'(\tau) - i\omega\tau\Big\}\Bigg|^2,](../../../images/math/1/7/3/17349ac690f28b6919f8fb5e4bc35d77.png)
![\mathcal{I}\equiv\int_0^T\!d\tau\,\Big[v'_x(\tau)\mathbf{\hat{e}}_x + v'_y(\tau)\mathbf{\hat{e}}_y\Big]\exp\Big\{ik_z z'(\tau) - i\omega\tau\Big\}
= \mathcal{I}_x\mathbf{\hat{e}}_x + \mathcal{I}_y\mathbf{\hat{e}}_y,](../../../images/math/2/0/4/2047ba341d57f8502ca4def6b78d021f.png)
![\mathcal{I}_x = \int_0^T\!d\tau\,v'_x(\tau)\exp\Big\{ik_z z'(\tau) - i\omega\tau\Big\}
= \frac{ca_w}{\gamma}\int_0^T\!d\tau\,\cos[k_wz'(\tau)]\exp\Big\{ik_z z'(\tau) - i\omega\tau\Big\}](../../../images/math/2/4/e/24e43ccf11bcb5c971fa76c481b54738.png)
![\mathcal{I}_y = \int_0^T\!d\tau\,v'_y(\tau)\exp\Big\{ik_z z'(\tau) - i\omega\tau\Big\}
= \frac{ca_w}{\gamma}\int_0^T\!d\tau\,\sin[k_wz'(\tau)]\exp\Big\{ik_z z'(\tau) - i\omega\tau\Big\}.](../../../images/math/3/6/e/36effb05cabb7030b19da886d6f1a12d.png)
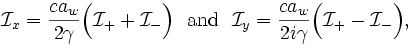
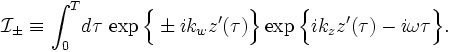
![\mathcal{I}_{\pm} = e^{i(k_z\pm k_w)z}\int_0^T\!d\tau\,\exp\Big\{-i[\omega - (k_z\pm k_w)v_z]\tau\Big\},](../../../images/math/9/7/8/978c8171063d31805221389ee43ed0fb.png)
![\mathcal{I}_{\pm} = - \frac{e^{i(k_z\pm k_w)z}}{i[\omega - (k_z\pm k_w)v_z]}\exp\Big\{-i[\omega - (k_z\pm k_w)v_z]\tau\Big\}\bigg|_0^T.](../../../images/math/b/e/5/be5f2c743674415085ab328c840912d7.png)
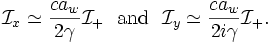
![\displaystyle\omega_{eff}\equiv\frac{1}{2}\Big[\omega - (k_z + k_w)v_z \Big],](../../../images/math/5/b/0/5b06adf936c33d894f30cad83a6ef9de.png)
![\mathcal{I}_{+} = -\frac{e^{i(k_z+k_w)z}}{2i\omega_{eff}}e^{-2i\omega_{eff}\tau}\bigg|_0^T
= -\frac{e^{i(k_z+k_w)z}}{2i\omega_{eff}}\bigg[e^{-2i\omega_{eff}T} - 1 \bigg].](../../../images/math/8/4/4/844583672bc3ed3db1a45fab4e270195.png)
![\mathcal{I}_{+} = \frac{1}{\omega_{eff}}e^{i(k_z+k_w)z}e^{-i\omega_{eff}T}\left\{\frac{1}{2i}\bigg[e^{i\omega_{eff}T} - e^{-i\omega_{eff}T} \bigg]\right\}
= Te^{i(k_z+k_w)z}e^{-i\omega_{eff}T}\left[\frac{\sin(\omega_{eff}T)}{\omega_{eff}T}\right]](../../../images/math/5/2/0/520ad8c2132260f6ffafdc83081e06a2.png)
![\eta(\omega) = \frac{e^2\omega^2}{4\pi^2c^3T}\big|\mathcal{I}\big|^2 = \frac{e^2\omega^2}{4\pi^2c^3T}\bigg[\big|\mathcal{I}_x\big|^2 + \big|\mathcal{I}_y\big|^2\bigg]
= \frac{e^2\omega^2}{4\pi^2c^3T}\bigg[\frac{c^2a_w^2}{2\gamma^2}\big|\mathcal{I}_+\big|^2\bigg]
= \frac{e^2\omega^2a_w^2T}{8\pi^2c\gamma^2}\frac{1}{T^2}\big|\mathcal{I}_+\big|^2.](../../../images/math/7/d/8/7d8d3370052fd9dcc1ebbd5177453424.png)
![\eta(\omega) \equiv \frac{1}{T}\frac{d^2I}{d\omega d\Omega} = \frac{e^2\omega^2a_w^2T}{8\pi^2c\gamma^2}\left[\frac{\sin^2(\omega_{eff}T)}{(\omega_{eff}T)^2}\right],](../../../images/math/5/3/8/538951f78c2540a9ffa6c31cc15d7f3b.png)
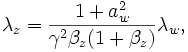
![\omega_{eff} = \frac{1}{2}\Big[\omega - (k_z + k_w)v_z \Big]
= \frac{1}{2}\left[\frac{2\pi c}{\lambda_z} - \left(\frac{2\pi}{\lambda_z} + \frac{2\pi}{\lambda_w}\right)v_z \right]
= \pi\left[\frac{1}{\lambda_z}\big(c-v_z\big) - \frac{1}{\lambda_w}v_z \right] = 0](../../../images/math/d/4/a/d4aa502b2f0f9f45cf94e3670444a0ce.png)