Integrating under the Integral Sign

From QED

< PlasmaWiki(Link to this page as [[PlasmaWiki/Integrating under the Integral Sign]])
Jump to: navigation, search

There exist situations where integration can be aided by the integration of a integrand with respect to some variable which you ordinarily wouldn't be interested in.

Mathworld gives an example, and there are more to follow.

This technique relies on the fact that integration is commutative. I'm guessing that this is -not- true for certain obscure or pathological functions. In that case, you'll probably have to think of something else. Don't say we didn't warn you.

Mathworld's example (I admit this is kind of backwards. I'm still working on a way to find intuition that would tell me that this is sensible before I do it):

For α > − 1

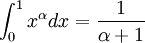
\int_{0}^{1} x^\alpha dx = \frac{1}{\alpha + 1}

Multiplying by dα and integrating α over [a,b]

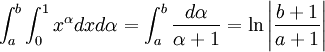
\int_{a}^{b} \int_{0}^{1} x^\alpha dx d \alpha = \int_{a}^{b} \frac{d \alpha}{\alpha + 1} = \ln{\left|{\frac{b + 1}{a + 1}}\right|}

But since we can switch the order of integration, the left hand side equals

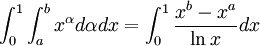
\int_{0}^{1} \int_{a}^{b} x^\alpha d \alpha dx = \int_{0}^{1} \frac{x^b - x^a}{\ln x} dx

So it follows that

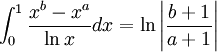
\int_{0}^{1} \frac{x^b - x^a}{\ln x} dx = \ln{\left|{\frac{b + 1}{a + 1}}\right|}

Which one might claim is non-obvious. (Note, Mathworld drops the absolute value function. Can anyone see why? I think it's merely a typo.)

Weisstein, Eric W. "Integration Under the Integral Sign." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/IntegrationUndertheIntegralSign.html

This page was recovered in October 2009 from the Plasmagicians page on Integrating_under_the_Integral_Sign dated 02:48, 30 September 2006.

Retrieved from "https://qed.princeton.edu/main/PlasmaWiki/Integrating_under_the_Integral_Sign"
Personal tools