Warning: jsMath requires JavaScript to process the mathematics on this page.
If your browser supports JavaScript, be sure it is enabled.

Landau Damping

From QED

< PlasmaWiki(Link to this page as [[PlasmaWiki/Landau Damping]])

Jump to: navigation, search

Valid regimes of Landau damping:

Bounce period of a particle should be shorter than wave damping time

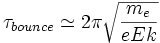
$\tau_{bounce} \simeq 2 \pi \sqrt{\frac{m_e}{e E k}}$

Summary of Landau Damping

1. Take a box

2. Cut a hole in the box

3. Start with Vlasov; Fourier in space, Laplace in time. This yields an expression for 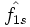$\hat{f_{1s}}$

4. From 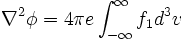$\nabla^2 \phi = 4\pi e \int_{-\infty}^{\infty}f_1 d^3v$ , eliminate 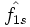$\hat{f_{1s}}$ from (3)

5. This yields 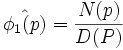$\hat{\phi_{1}(p)}=\frac{N(p)}{D(P)}$

6. Inverse Laplace transform: 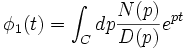$\phi_{1}(t) = \int_{C} dp \frac{N(p)}{D(p)} e^{pt}$ . The contour C is originally the Bromwich countour, which can be deformed into a region $p < p 0$ where 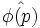$\hat{\phi(p)}$ is not defined. For $R e (p) < 0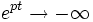$ , $e^{pt}\rightarrow -\infty$ , so $φ 1 (t)$ is defined only by the poles.

7. Argue that $N (p)$ does not have any poles. Thus all the poles of 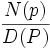$\frac{N(p)}{D(P)}$ come from the zeros of $D (p)$ This gives the dispersion function:

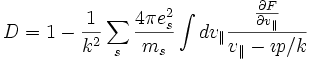
$D=1-\frac{1}{k^2}\sum_s \frac{4\pi e_s^2}{m_s}\int dv_{\parallel} \frac{ \frac{\partial F}{\partial v_{\parallel}} } {v_{\parallel}-\imath p/k }$

8. The behavior of 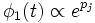$\phi_{1}(t)\propto e^{p_j}$ will be dominated by the zero $p j$ of $D$ with the greatest real part. This will correspond to the mode with the higher growth or lowest damping.

9. Evaluating D requires an integration in 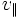$v_{\parallel}$ along a Landau contour. To get the proper contour remember that in the definition of Laplace transform, $p > 0$ . Thus the pole in D is initially above the real axis. As p is allowed to become negative, the pole will descend crossing the real axis at some point. The contour then must be indented downwards to preserve analyticity of D.