QM M00 1
From QED
Consider a spin- particle constrained to move on a 1D
line with a harmonic oscillator potential and a
magnetic field so that the Hamiltonian is:
particle constrained to move on a 1D
line with a harmonic oscillator potential and a
magnetic field so that the Hamiltonian is:
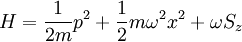
The first energy level is not degenerate but all the other levels are doubly degenerate.
Now add a small magnetic field in the 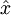 direction with a
magnitude proportional to x . The Hamiltonian is:
direction with a
magnitude proportional to x . The Hamiltonian is:
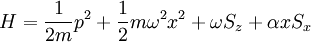
Calculate the energy difference in the levels to lowest order.
Define the original the Hamiltonian:
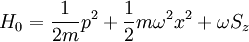
And add the perturbation:
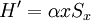
We define the basis of eigenstates of H0 to be 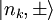 , where nk
is the quantum number for the kinetic energy, and
, where nk
is the quantum number for the kinetic energy, and 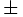 defines either the + or - spin state. The energy from
the state is
defines either the + or - spin state. The energy from
the state is 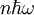 .
.
Since we know:
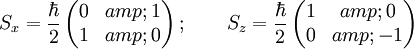
so that the properties of Sx are:

We can also decompose the x operator:
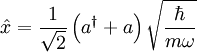
where a and 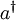 are the annhiliation and creation
operators. The energy perturbation to first order is
given by:
are the annhiliation and creation
operators. The energy perturbation to first order is
given by:
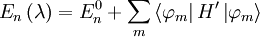
Where we must diagonalize the states:
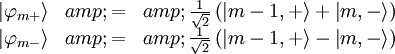
So the change in energy is given by:
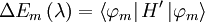
Now it simply remains to calculate the values
of 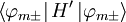 :
:
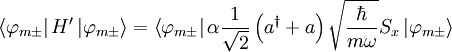
So that for 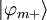 :
:
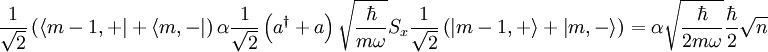
And for 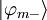 :
:
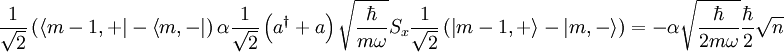
So that the total energy difference is just given by:
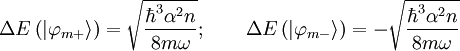
We must treat the ground state separately, since it is nondegenerate. We must take it out to second order:
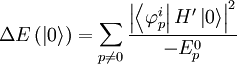
Finding the nonzero values of this, we get:
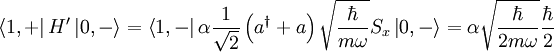
as the only one. Thus:
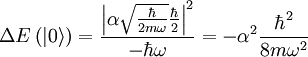
At last we get:
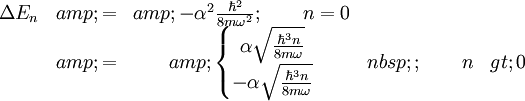
where the pair for n > 0 indicates the splitting of a degenerate pair.
This page was recovered in October 2009 from the Plasmagicians page on Prelim_M00_QM1 dated 22:28, 23 December 2005.












