Warning: jsMath requires JavaScript to process the mathematics on this page.
If your browser supports JavaScript, be sure it is enabled.

QM M04 2

From QED

< PlasmaWiki(Link to this page as [[PlasmaWiki/Old Prelims/QM M04 2]])

Jump to: navigation, search

The Hamiltonian is:

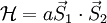
$\mathcal{H}=a\vec{S}_{1}\cdot\vec{S}_{2}$

Which we can rewrite using the dot product of the spin operator:

$\mathcal{H}=\frac{a}{2}\left[J^{2}-S_{1}^{2}-S_{2}^{2}\right]$

Particle 1 has spin S, particle 2 has spin 1/2, so we will get:

$E=\frac{a}{2}\left[j(j+1)\hbar^{2}-S(S+1)\hbar^{2}-\frac{3\hbar^{2}}{4}\right]$

The total spin 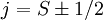$j=S\pm1/2$ :

$E=\frac{a\hbar^{2}}{2}\left[\left(S\pm\frac{1}{2}\right)\left(S\pm\frac{1}{2}+1\right)-S(S+1)-\frac{3}{4}\right]$ $E=\frac{a\hbar^{2}}{2}\left[S^{2}\pm\frac{S}{2}+S\pm\frac{S}{2}+\frac{1}{4}\pm\frac{1}{2}-S^{2}-S-\frac{3}{4}\right]=\frac{a\hbar^{2}}{2}\left[\pm S\pm\frac{1}{2}-\frac{1}{2}\right]$

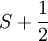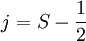The energy $S+\frac{1}{2}$ (thus taking on $2 S + 2$ states), while $j=S-\frac{1}{2}$ , so it takes on $2 S$ states.

Since we have two spin 1/2 particles, we can express every state as the up or down of each of the two particles:

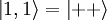
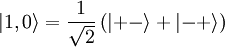
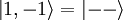
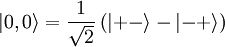
$\left|1,1\right\rangle =\left|++\right\rangle$ $\left|1,0\right\rangle =\frac{1}{\sqrt{2}}\left(\left|+-\right\rangle +\left|-+\right\rangle \right)$ $\left|1,-1\right\rangle =\left|--\right\rangle$ $\left|0,0\right\rangle =\frac{1}{\sqrt{2}}\left(\left|+-\right\rangle -\left|-+\right\rangle \right)$

We apply the hamiltonian (and use our knowledge of Pauli Matrices to apply $S x$ and $S y$ to $S z$ eigenstates):

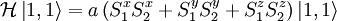
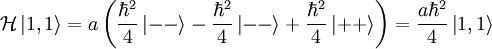
$\mathcal{H}\left|1,1\right\rangle =a\left(S_{1}^{x}S_{2}^{x}+S_{1}^{y}S_{2}^{y}+S_{1}^{z}S_{2}^{z}\right)\left|1,1\right\rangle$ $\mathcal{H}\left|1,1\right\rangle =a\left(\frac{\hbar^{2}}{4}\left|--\right\rangle -\frac{\hbar^{2}}{4}\left|--\right\rangle +\frac{\hbar^{2}}{4}\left|++\right\rangle \right)=\frac{a\hbar^{2}}{4}\left|1,1\right\rangle$

And:

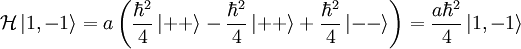
$\mathcal{H}\left|1,-1\right\rangle =a\left(\frac{\hbar^{2}}{4}\left|++\right\rangle -\frac{\hbar^{2}}{4}\left|++\right\rangle +\frac{\hbar^{2}}{4}\left|--\right\rangle \right)=\frac{a\hbar^{2}}{4}\left|1,-1\right\rangle$

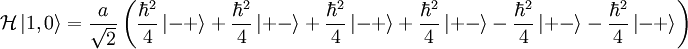
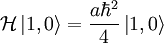
$\mathcal{H}\left|1,0\right\rangle =\frac{a}{\sqrt{2}}\left(\frac{\hbar^{2}}{4}\left|-+\right\rangle +\frac{\hbar^{2}}{4}\left|+-\right\rangle +\frac{\hbar^{2}}{4}\left|-+\right\rangle +\frac{\hbar^{2}}{4}\left|+-\right\rangle -\frac{\hbar^{2}}{4}\left|+-\right\rangle -\frac{\hbar^{2}}{4}\left|-+\right\rangle \right)$ $\mathcal{H}\left|1,0\right\rangle =\frac{a\hbar^{2}}{4}\left|1,0\right\rangle$

Lastly:

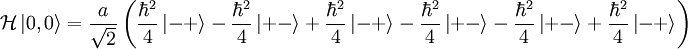
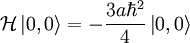
$\mathcal{H}\left|0,0\right\rangle =\frac{a}{\sqrt{2}}\left(\frac{\hbar^{2}}{4}\left|-+\right\rangle -\frac{\hbar^{2}}{4}\left|+-\right\rangle +\frac{\hbar^{2}}{4}\left|-+\right\rangle -\frac{\hbar^{2}}{4}\left|+-\right\rangle -\frac{\hbar^{2}}{4}\left|+-\right\rangle +\frac{\hbar^{2}}{4}\left|-+\right\rangle \right)$ $\mathcal{H}\left|0,0\right\rangle =-\frac{3a\hbar^{2}}{4}\left|0,0\right\rangle$

So the eigenvalue 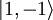$\left|1,-1\right\rangle$ , while the eigenvalue 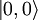$\left|0,0\right\rangle$ .

We use the same eigenvectors as they are all eigenvectors of $S z$ . Finding eigenvalues:

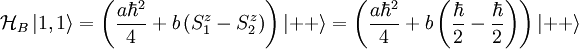
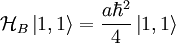
$\mathcal{H}_{B}\left|1,1\right\rangle =\left(\frac{a\hbar^{2}}{4}+b\left(S_{1}^{z}-S_{2}^{z}\right)\right)\left|++\right\rangle =\left(\frac{a\hbar^{2}}{4}+b\left(\frac{\hbar}{2}-\frac{\hbar}{2}\right)\right)\left|++\right\rangle$ $\mathcal{H}_{B}\left|1,1\right\rangle =\frac{a\hbar^{2}}{4}\left|1,1\right\rangle$

Similarly:

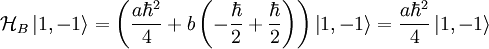
$\mathcal{H}_{B}\left|1,-1\right\rangle =\left(\frac{a\hbar^{2}}{4}+b\left(-\frac{\hbar}{2}+\frac{\hbar}{2}\right)\right)\left|1,-1\right\rangle =\frac{a\hbar^{2}}{4}\left|1,-1\right\rangle$

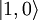For $\left|1,0\right\rangle$ :

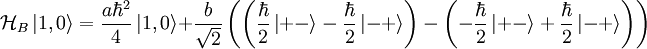
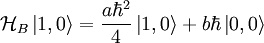
$\mathcal{H}_{B}\left|1,0\right\rangle =\frac{a\hbar^{2}}{4}\left|1,0\right\rangle +\frac{b}{\sqrt{2}}\left(\left(\frac{\hbar}{2}\left|+-\right\rangle -\frac{\hbar}{2}\left|-+\right\rangle \right)-\left(-\frac{\hbar}{2}\left|+-\right\rangle +\frac{\hbar}{2}\left|-+\right\rangle \right)\right)$ $\mathcal{H}_{B}\left|1,0\right\rangle =\frac{a\hbar^{2}}{4}\left|1,0\right\rangle +b\hbar\left|0,0\right\rangle$

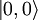For $\left|0,0\right\rangle$ :

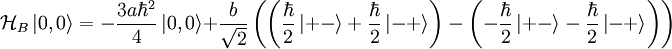
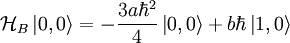
$\mathcal{H}_{B}\left|0,0\right\rangle =-\frac{3a\hbar^{2}}{4}\left|0,0\right\rangle +\frac{b}{\sqrt{2}}\left(\left(\frac{\hbar}{2}\left|+-\right\rangle +\frac{\hbar}{2}\left|-+\right\rangle \right)-\left(-\frac{\hbar}{2}\left|+-\right\rangle -\frac{\hbar}{2}\left|-+\right\rangle \right)\right)$ $\mathcal{H}_{B}\left|0,0\right\rangle =-\frac{3a\hbar^{2}}{4}\left|0,0\right\rangle +b\hbar\left|1,0\right\rangle$

If we only consider these two states, then:

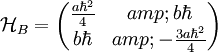
$\mathcal{H}_{B}=\left(\begin{matrix} \frac{a\hbar^{2}}{4} & b\hbar\\ b\hbar & -\frac{3a\hbar^{2}}{4}\end{matrix}\right)$

Which gives us the determinant:

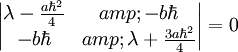
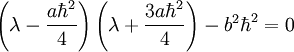
$\left|\begin{matrix} \lambda-\frac{a\hbar^{2}}{4} & -b\hbar\\ -b\hbar & \lambda+\frac{3a\hbar^{2}}{4}\end{matrix}\right|=0$ $\left(\lambda-\frac{a\hbar^{2}}{4}\right)\left(\lambda+\frac{3a\hbar^{2}}{4}\right)-b^{2}\hbar^{2}=0$

Which has solutions 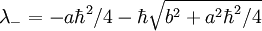$\lambda_{-}=-a\hbar^{2}/4-\hbar\sqrt{b^{2}+a^{2}\hbar^{2}/4}$ . I will not find the normalized eigenstates because it is not fun.