SM J04 1
From QED
Consider N non-interacting quantized spins in a
magnetic field 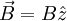 . The energy of the spins is − BMz, where:
. The energy of the spins is − BMz, where:
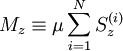
is the total magnetization. For each spin, 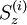 takes only 2S+1
values -S, -S+1, ..., S-1, S. Given the temperature of
the system T:
takes only 2S+1
values -S, -S+1, ..., S-1, S. Given the temperature of
the system T:
a. Calculate the Gibbs partition function Z(T,B);
b. Calculate the Gibbs free energy G(T,B) and evaluate
its asymptotic behavior at weak ( 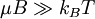 )
magnetic field;
)
magnetic field;
c. Calculate the zero-field magnetic susceptibility
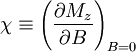
d. Calculate the magnetic susceptibility at strong
fields 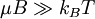 .
.
The partition function for one particle is given by:
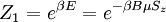
We can get the expectation of Sz by:
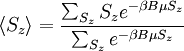
Where the sums are over all possible values of Sz. Using this, we get the total partition function to be:
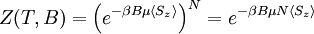
The Gibbs free energy may be found by:
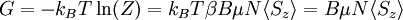
In the case that 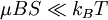 , eβμBS˜1, and so we find:
, eβμBS˜1, and so we find:
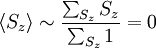
so that the Gibbs free energy 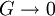 .
.
In the other case that 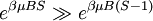 , so:
, so:
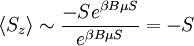
and the Gibbs free energy 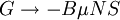 .
.
The magnetic susceptibility is defined by:
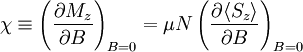
Taking the derivative
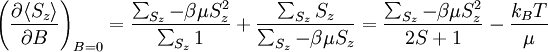
Plugging in:
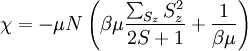
1.1.4 Part d
This is similar to the last part, but we get:
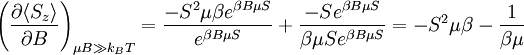
So that:
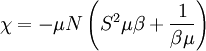
This page was recovered in October 2009 from the Plasmagicians page on Prelim_J04_SMT1 dated 02:24, 13 August 2006.












