CM J00 1

From QED

< PlasmaWiki | Prelims(Link to this page as [[PlasmaWiki/Prelims/CM J00 1]])
Jump to: navigation, search

This is a completed problem. Please read this talk page and discuss substantial changes here before making them. Alternative solutions may be posted before discussion on this page. However, if the results disagree, discussion is encouraged.

This is a debated topic, which may be under dispute. These solutions have some debate over the correct solution. Please remove them from the category once the debate is resolved (and please debate in the discussion tab, rather than the main article).

Solution 1

Image:PlasmaWiki_Jan00-CM1.jpg


Soultion 2

The shape of an arch is determined by the condition that each brick is held in place by the normal force of it's neighbours, with no need for mortar or "glue". To model this consider a thin course of bricks shared so the normal force exerted on each brick by the neighbour on either side supports the brick against the uniform graviational acceleration g. Then imagine the limit where the arch is a thin line with height y = y(x) as a function of horizontal position x. The constant mass per unit length along the line of the arch is μ.

Find y(x) for an arch with horizontal width 2l and height h. Give the equations that determine the constants in your solution, but you need not solve for the constants.

The first thing to note is: Read the question! I managed to miss that we didn't need to solve for the constants the first time.

One can find the solution very easily by transforming the problem. Consider a single brick. It cannot sustain any shear force at it's contact point by hypothesis (normal force only, not friction). We also know that the normal force downward exactly repels the total mass of the brick and half those above it, and we know the direction of the normal force.

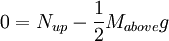
0=N_{up}-\frac{1}{2}M_{above}g

We note that is picture is completely static: we can flip the y axis. Here's what changes 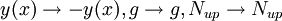y(x) \rightarrow -y(x), g \rightarrow g, N_{up} \rightarrow N_{up}. Now the normal force is directed outward along the curve, opposing gravity and the normal force from the opposite side. The constaint that there is no shear force keeps the normal force directed along the curve: the normal force has been translated into tension!

The question has been translated into finding the shape of a hanging wire: a catenary.

Note: I will use the terms arch and string interchangably, as they're the same thing in this limit.

The horizontal force of an arch element is balanced on both sides: therefore, it is constant across the string. Call this FH. The force is, as per sensibility, directed along the string. Hence:

|\vec{F}| = \sec\theta F_H and FV = tanθFH

Now we balance the vertical forces. Since there is a dominant first order derivative, it doesn't matter where we stick the endpoints, so call them a,b with θ,θ + dθ. Thus:

FHtanθ + μgdl = FHtan(θ + dθ)
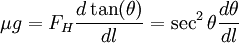
\mu g = F_H\frac{d\tan(\theta)}{dl} = \sec^2\theta \frac{d\theta}{dl}
Or
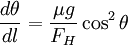
\frac{d\theta}{dl}=\frac{\mu g}{F_H}\cos^2\theta

Here, we have the wonderful relation 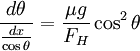\frac{d\theta}{\frac{dx}{\cos\theta}}=\frac{\mu g}{F_H}\cos^2\theta, leading to:

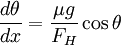
\frac{d\theta}{dx}=\frac{\mu g}{F_H}\cos\theta
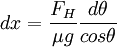
dx=\frac{F_H}{\mu g}\frac{d\theta}{cos\theta}

We want x in terms of y, because we can then solve the initial value problem. We note that 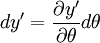dy' = \frac{\partial y'}{\partial \theta}d\theta.

We also have 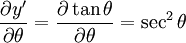\frac{\partial y'}{\partial \theta} = \frac{\partial \tan\theta}{\partial \theta} = \sec^2\theta

We can now use the replacement rule dθ = cos2θdy' yielding

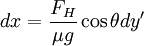
dx = \frac{F_H}{\mu g} \cos\theta dy'
Removing the cosθ.
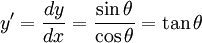
y' = \frac{dy}{dx} = \frac{\sin\theta}{\cos\theta} = \tan\theta
sec2θ = 1 + tan2θ = 1 + y'2
Yielding
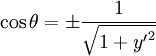
\cos\theta = \pm \frac{1}{\sqrt{1 + {y'}^2}}

So that

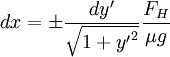
dx = \pm \frac{dy'}{\sqrt{1 + {y'}^2}}\frac{F_H}{\mu g}

Integrating from ycenter to yhigh and xcenter to xendpoint, where dx,dy' > 0

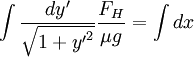
\int{\frac{dy'}{\sqrt{1 + {y'}^2}}\frac{F_H}{\mu g}} = \int{dx}

Thus

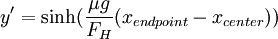
y' = \sinh(\frac{\mu g}{F_H} (x_{endpoint} - x_{center}))

and

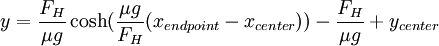
y = \frac{F_H}{\mu g} \cosh(\frac{\mu g}{F_H} (x_{endpoint} - x_{center})) - \frac{F_H}{\mu g} + y_{center}

Flipping the y-axis back to an arch (instead of a catenary), we have

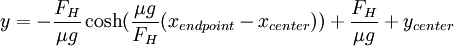
y = - \frac{F_H}{\mu g} \cosh(\frac{\mu g}{F_H} (x_{endpoint} - x_{center})) + \frac{F_H}{\mu g} + y_{center}

At the arch's maximum height h, x = l so that 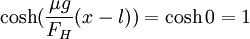\cosh(\frac{\mu g}{F_H} (x - l)) = \cosh 0 = 1. ycenter is thus

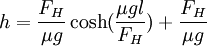
h = \frac{F_H}{\mu g} \cosh(\frac{\mu g l}{F_H}) + \frac{F_H}{\mu g}

off the ground.

Where M is the total weight of the arch, the final constant is given by
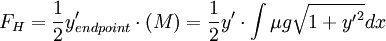
F_H = \frac{1}{2}y'_{endpoint} \cdot (M) = \frac{1}{2}y' \cdot \int{\mu g \sqrt{1 + {y'}^2} dx}

We are not required to evaluate this integral, as the weight of the arch is not requested. So, finally we have arrived at our desired solution.

This page was recovered in October 2009 from the Plasmagicians page on Prelim_J00_Mech1 dated 21:39, 5 July 2007.

Retrieved from "https://qed.princeton.edu/main/PlasmaWiki/Prelims/CM_J00_1"
Personal tools