CM J04 1

From QED

< PlasmaWiki | Prelims(Link to this page as [[PlasmaWiki/Prelims/CM J04 1]])
Jump to: navigation, search

A bead of mass m slides without friction on a wire whose shape is

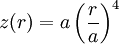
z(r)=a\left(\frac{r}{a}\right)^{4}

The wire rotates about the z axis with constant angular velocity ω. Earth's gravity causes acceleration g in the negative z direction

a. Find the equation of motion for the bead in terms of coordinate r

b. Find the equilibrium points. Say whether each is stable.

c. For the stable equilibria, find the frequency of small oscillations about equilibrium.

We can define the angle that the wire makes with the horizontal by:

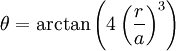
\theta=\arctan\left(4\left(\frac{r}{a}\right)^{3}\right)

Then the forces are easy to write:

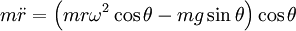
m\ddot{r}=\left(mr\omega^{2}\cos\theta-mg\sin\theta\right)\cos\theta

Removing θ, we get 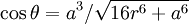\cos\theta=a^{3}/\sqrt{16r^{6}+a^{6}}. Thus:

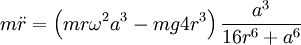
m\ddot{r}=\left(mr\omega^{2}a^{3}-mg4r^{3}\right)\frac{a^{3}}{16r^{6}+a^{6}}

Since r>0 and a>0 , stable points exist where:

mrω2a3 = mg4r3

So that r0 = 0 is an equilibrium point, as well as:

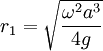
r_{1}=\sqrt{\frac{\omega^{2}a^{3}}{4g}}

It is easy to see that r0 is unstable, and that r1 is stable, but we can prove it by finding the equation of motion for ri + δr:

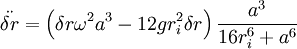
\ddot{\delta r}=\left(\delta r\omega^{2}a^{3}-12gr_{i}^{2}\delta r\right)\frac{a^{3}}{16r_{i}^{6}+a^{6}}

So that for r0:

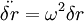
\ddot{\delta r}=\omega^{2}\delta r

Which is positive so unstable, and for r1:

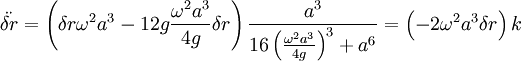
\ddot{\delta r}=\left(\delta r\omega^{2}a^{3}-12g\frac{\omega^{2}a^{3}}{4g}\delta r\right)\frac{a^{3}}{16\left(\frac{\omega^{2}a^{3}}{4g}\right)^{3}+a^{6}}=\left(-2\omega^{2}a^{3}\delta r\right)k

where k is the large fraction sticking out, which is strictly positive. Since this is negative, oscillations are stable

We already found:

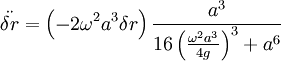
\ddot{\delta r}=\left(-2\omega^{2}a^{3}\delta r\right)\frac{a^{3}}{16\left(\frac{\omega^{2}a^{3}}{4g}\right)^{3}+a^{6}}

So that the frequency of oscillations is:

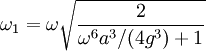
\omega_{1}=\omega\sqrt{\frac{2}{\omega^{6}a^{3}/(4g^{3})+1}}

This page was recovered in October 2009 from the Plasmagicians page on Prelim_J04_Mech1 dated 17:43, 1 January 2006.

Retrieved from "https://qed.princeton.edu/main/PlasmaWiki/Prelims/CM_J04_1"
Personal tools