CM M01 1

From QED

< PlasmaWiki | Prelims(Link to this page as [[PlasmaWiki/Prelims/CM M01 1]])
Jump to: navigation, search

First Solution

PlasmaWiki_Prelims_CM_M01_1.pdf (help ยท info)

Second Solution

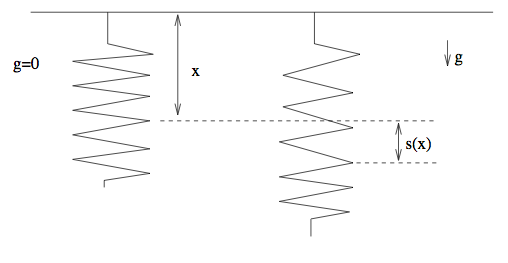
A spring has spring constant K , unstretched length L , and mass per unit length ρ. The spring is suspended vertically from one end in a constant gravitational field, g , and stretches under its own weight.

a. For a point whose distance from the upper end of the spring is x when unstretched, find its distance s(x) from the initial position x when the spring is stretched (ed: bold to show emphasize change from real text to match picture)

b. Suppose we suddenly 'turn off' gravity. (This can be done for example by putting the system in an elevator, which suddenly falls down freely from rest.) Find the subsequent motion s(x,t) of the spring.

We can write the force equation on length Δx (Using T(x) as the tension):

T(x + Δx) − T(x) + ρgΔx = 0
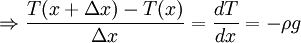
\Rightarrow\frac{T(x+\Delta x)-T(x)}{\Delta x}=\frac{dT}{dx}=-\rho g

solving this for T(x):

T(x) = − ρgx + const

we find the constant by T(L)=0:

T(x) = ρg(L − x)

Now consider finding the tension by the amount that Δx stretches. Its change in length will be s(x + Δx) − s(x), which gives the tension:

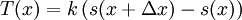
T(x)=k\left(s(x+\Delta x)-s(x)\right)

The spring constant will change since we shortened the length:

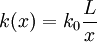
k(x)=k_{0}\frac{L}{x}

so that:

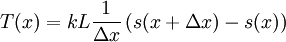
T(x)=kL\frac{1}{\Delta x}\left(s(x+\Delta x)-s(x)\right)

which defines the tension as:

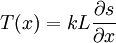
T(x)=kL\frac{\partial s}{\partial x}

Setting the two tensions equal:

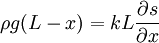
\rho g(L-x)=kL\frac{\partial s}{\partial x}
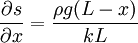
\frac{\partial s}{\partial x}=\frac{\rho g(L-x)}{kL}

Integrating, we find:

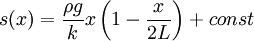
s(x)=\frac{\rho g}{k}x\left(1-\frac{x}{2L}\right)+const

We must have s(0)=0 for it to stay at the top, so this constant is zero:

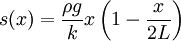
s(x)=\frac{\rho g}{k}x\left(1-\frac{x}{2L}\right)

We can write:

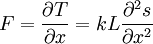
F=\frac{\partial T}{\partial x}=kL\frac{\partial^{2}s}{\partial x^{2}}
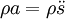
\rho a=\rho\ddot{s}

Putting it together:

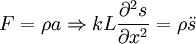
F=\rho a\Rightarrow kL\frac{\partial^{2}s}{\partial x^{2}}=\rho\ddot{s}

Which is a familiar wave equation, with solutions of the form:

s(x,t) = f(x − vt) + g(x + vt)

with v2 = kL / ρ given by the wave equation. Using the boundary condition at t=0 , we know we must have the solution from part a. Therefore:

s(x,0) = f(x) + g(x)

We also assume that the spring was at rest:

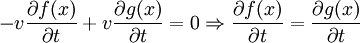
-v\frac{\partial f(x)}{\partial t}+v\frac{\partial g(x)}{\partial t}=0\Rightarrow\frac{\partial f(x)}{\partial t}=\frac{\partial g(x)}{\partial t}

The only way for this to be true is to have f(x) = g(x) = s(x,0) / 2 at t=0:

Failed to parse (syntax error): f(x)=g(x)=\frac{\rho g}{2k}x\left(1-\frac{x}{2L}\right);\qquad0&lt;x&lt;L

We need to extend g to x>L , and can do so by noting that 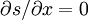\partial s/\partial x=0 at x=L . Thus:

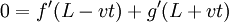
0=f^{\prime}(L-vt)+g^{\prime}(L+vt)

which means that 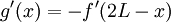g^{\prime}(x)=-f^{\prime}(2L-x) for x>L . Integrating, we get g(x > L) = − f(2L − x). Lastly, we must have s(0,t)=0 for all t :

0 = f( − vt) + g(vt)

So we can extend the regime of x to x<0 using this, just by saying that f(x < 0) = − g( − x).

These two combine recursively to give us: 

<math>s(x,t)=f(x-vt)+g(x+vt)\,</math>

<math>f(x)=g(x)=\left\{ \begin{matrix} -h(-x) & ;\quad & x<0\\ h(x) & ;\quad & 0\leq x\leq L\\ h(2L-x) & ;\quad & L<x\end{matrix}\right.</math>
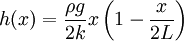
h(x)=\frac{\rho g}{2k}x\left(1-\frac{x}{2L}\right)

This page was recovered in October 2009 from the Plasmagicians page on Prelim_M01_Mech1 dated 18:10, 24 April 2006.

Retrieved from "https://qed.princeton.edu/main/PlasmaWiki/Prelims/CM_M01_1"
Personal tools