CM M01 2
From QED
A particle fo mass m moves in a one-dimensional potential V(x) = − ax2 + bx4 with very light damping. The particle is set in motion with a large initial velocity. Suppose now we measure the period of the motion for each full oscillation, and call these periods T1, T2, T3, T4, and so on. It is observed that the Ti briefly became very large for i near some i0.
a. Explain what makes the periods get large
b. Obtain a scaling form for Ti near i = i0, valid in the limit
of small damping. (A scaling form would be something
like 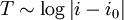 , etc). Hint: Consider first the
miton without the friction,
, etc). Hint: Consider first the
miton without the friction, 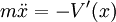 . Recalling that this
motion is necessarily periodic, derive an integral
formula relating the period of oscillation to the
energy and the turning points x − and x + of the motion.
. Recalling that this
motion is necessarily periodic, derive an integral
formula relating the period of oscillation to the
energy and the turning points x − and x + of the motion.
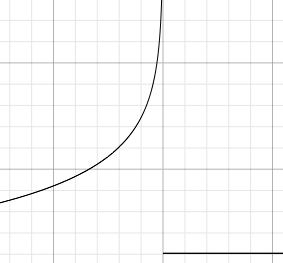
c. Give an approximate sketch of Ti as a function of i.
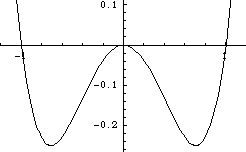
The potential looks like (in this graph a=b=1):
The periods get large because there is the hump in the middle, coming from the − bx2 term, which dominates for sufficiently small x. Particles with nearly zero energy will have very small velocity here, and so spend a lot of time (since there is only small acceleration as well). This is why the periods become large.
We can write down energy conservation for each period, assuming damping is small:
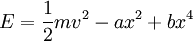
solving for the velocity:
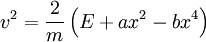
So we can find the period by:
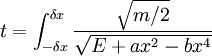
If we take δx of the integration to be 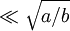 , we can neglect
the x4 term, and get:
, we can neglect
the x4 term, and get:
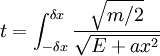
which we recognize as the arcsinh:
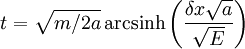
Considering δx fixed, when we reduce E we can rewrite the arcsinh:
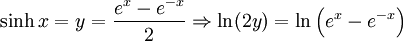
For large y, to get positive x, x must be large, which means:
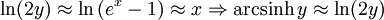
Plugging in:
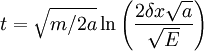
Only considering the dependence on E:
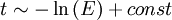
Now we consider the damping to be linear with rate \kappa :
where E0 is the initial energy. We can write the critical value of i as i0 = E0 / κ, so that Ei = κ(i0 − i), which gives the time dependence:
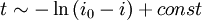
The period will increase to infinity as it approaches the critical period, and then flatten out as it enters harmonic oscillation:
This page was recovered in October 2009 from the Plasmagicians page on Prelim_M01_Mech2 dated 19:41, 20 December 2005.