CM M01 3
From QED
A particle of mass m and charge q moves freely in a
gravitational field 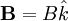 . At time t=0 ,
the particle is released from the origin O with no
initial velocity. It traces a curve in the x , y plane.
. At time t=0 ,
the particle is released from the origin O with no
initial velocity. It traces a curve in the x , y plane.
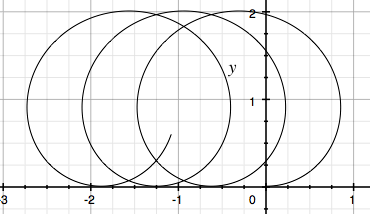
a. Find the parametric equations x=x(t), y=y(t) describing the curve. Sketch the curve on an x, y diagram.
The above motion is idealized, because two effects have been ignored: air drag and radiation damping
b. Now assume that the particle also feels a drag force due to the surrounding atmosphere, F = − βv. Derive the motion of the particle. What is its final velocity?
c. Instead of air drag, suppose we include the damping effect caused by the electromagnetic radiation emitted during its motion. Describe, qualitatively, how this modifies the motion found in part a. What is the final velocity of the particle?
We have the equations of motion:
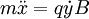
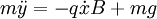
Dotting these, dividing by m, and substituting:
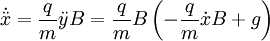
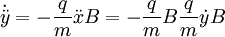
From these, we find the solutions have the form:
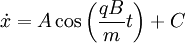
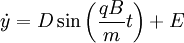
Solving for the constants, using 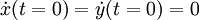 , we get:
, we get:
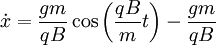
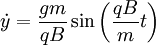
Integrating:
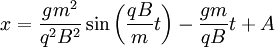
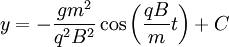
Solving for the constants such that x(t=0)=y(t=0)=0 :
<math>x=\frac{gm^{2}}{q^{2}B^{2}}\sin\left(\frac{qB}{m}t\right)-\frac{gm}{qB}t</math>
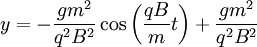
Which looks like a drifting loop:
The total force by the drag will be:
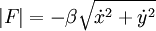
which means that in the x and y directions:

So we get the equations of motion:
<math>m\ddot{x}=q\dot{y}B-\beta\dot{x}</math>
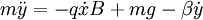
We can find the final velocity by finding 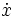 such
that these equations are zero:
such
that these equations are zero:
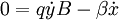
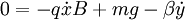
Plugging the first equation into the second:
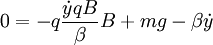
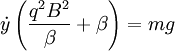
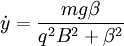
Giving:
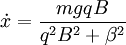
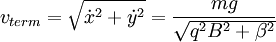
The radiation will only slow the motion perpendicular to the motion of the guiding center, since we can consider that in the frame of the guiding center it is moving in a circle and will come to rest. Once this radial motion has all been emitted, it will simply move with the guiding center velocity:
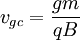
This page was recovered in October 2009 from the Plasmagicians page on Prelim_M01_Mech3 dated 21:20, 20 December 2005.