CM M03 1

From QED

< PlasmaWiki | Prelims(Link to this page as [[PlasmaWiki/Prelims/CM M03 1]])
Jump to: navigation, search

The earth is in a circular orbit of angular frequency \omega about the sun. The sun is so much more massive than the earth that, for our purposes, it may be taken to sit at rest at the center of our coordinate system. Lagrange discovered that there exist a certain number of equilibrium points at which an artificial satelite of negligible mass can orbit the sun with the same frequency ω as the earth (while maintaining a fixed distance from both the earth and the sun). Such orbits are ideally suited for space-based observatories of various kinds. We will explore some of the properties of the 'Lagrange points' in this problem.

a. Consider points on the line that runs from the sun through the earth. This line is of course stationary in the reference frame that rotates with the earth in its orbit. Show that there is one point on this line outside the earth's orbit where a test particle may sit at equilibrium in the rotating frame. This point is commonly designated as the L2 Lagrange point. (There is a similar Lagrange point, L1, inside the earth's orbit as well.)

b. Give an approximate expression, correct to leading order in the small quantity β = Me / Ms, for the distance from the earth to the L2 Lagrange point described above. Express your answer in terms of the masses and R, the earth-sun distance. The Wilkinson Microwave Anisotropy Probe (WMAP) is stationed at L2: using 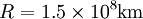R=1.5\times10^{8}\mathrm{km}, find the distance from earth to WMAP.

c. Determine whether the L2 equilibrium point is stable or unstable against small perturbations in position along the earth-sun line.

In the rotating frame, the gravity must provide the centripetal force:

Fc = mrω2

The force of gravity is:

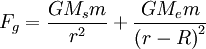
F_{g}=\frac{GM_{s}m}{r^{2}}+\frac{GM_{e}m}{\left(r-R\right)^{2}}

For equilibrium:

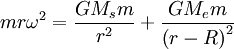
mr\omega^{2}=\frac{GM_{s}m}{r^{2}}+\frac{GM_{e}m}{\left(r-R\right)^{2}}

The left hand side of this equation is monotonically increasing, while for r>R , the RHS is monotonically decreasing from 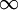\infty to 0. Therefore, there is one solution to this equation for r>R .

We can rearrange the equation:

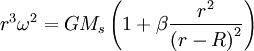
r^{3}\omega^{2}=GM_{s}\left(1+\beta\frac{r^{2}}{\left(r-R\right)^{2}}\right)

Taking the cube root of both sides, and expanding the cube root of what is in parenthesis in terms of small parameter β:

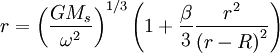
r=\left(\frac{GM_{s}}{\omega^{2}}\right)^{1/3}\left(1+\frac{\beta}{3}\frac{r^{2}}{\left(r-R\right)^{2}}\right)

We can make the replacement x=r-R , and abbreviate 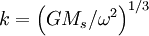k=\left(GM_{s}/\omega^{2}\right)^{1/3} to find the distance:

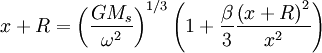
x+R=\left(\frac{GM_{s}}{\omega^{2}}\right)^{1/3}\left(1+\frac{\beta}{3}\frac{\left(x+R\right)^{2}}{x^{2}}\right)

Putting this in order, the distance x from the earth solves:

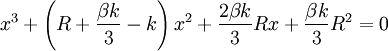
x^{3}+\left(R+\frac{\beta k}{3}-k\right)x^{2}+\frac{2\beta k}{3}Rx+\frac{\beta k}{3}R^{2}=0

The force equation is:

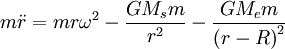
m\ddot{r}=mr\omega^{2}-\frac{GM_{s}m}{r^{2}}-\frac{GM_{e}m}{\left(r-R\right)^{2}}

Perturbing around a solution rL2, so that r = rL2 + δr:

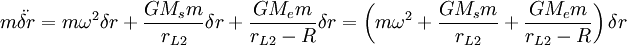
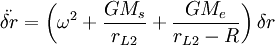
m\ddot{\delta r}=m\omega^{2}\delta r+\frac{GM_{s}m}{r_{L2}}\delta r+\frac{GM_{e}m}{r_{L2}-R}\delta r=\left(m\omega^{2}+\frac{GM_{s}m}{r_{L2}}+\frac{GM_{e}m}{r_{L2}-R}\right)\delta r \ddot{\delta r}=\left(\omega^{2}+\frac{GM_{s}}{r_{L2}}+\frac{GM_{e}}{r_{L2}-R}\right)\delta r

This coefficient is always positive (since rL2 is defined to be outside earth's orbit), so the solution is unstable.

This page was recovered in October 2009 from the Plasmagicians page on Prelim_M03_Mech1 dated 02:21, 13 August 2006.

Retrieved from "https://qed.princeton.edu/main/PlasmaWiki/Prelims/CM_M03_1"
Personal tools