CM M03 2
From QED
The problem of a sphere rolling without slipping directly down an inclined plane is an old chestnut of freshman physics. In this problem, you are asked to examine more general motions of a sphere rolling without slipping on inclined and rotating planes.
The state of motion of a sphere of mass M is specified
by giving its position 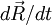 with respect to a
fixed point and its angular velocity
with respect to a
fixed point and its angular velocity 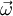 with respect to
its center of mass. The rolling without slipping
constraint is usually expressed as
with respect to
its center of mass. The rolling without slipping
constraint is usually expressed as 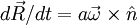 where a is the
sphere's radius and
where a is the
sphere's radius and 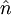 is the unit vector normal to the
plane on which the sphere is rolling. There is a
constraint force
is the unit vector normal to the
plane on which the sphere is rolling. There is a
constraint force 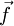 which acts in the plane to enforce
the constraint and this constraint force has to be
etaken into account in the equations for acceleration
of the center of mass and for time rate of change of
the angular momentum
which acts in the plane to enforce
the constraint and this constraint force has to be
etaken into account in the equations for acceleration
of the center of mass and for time rate of change of
the angular momentum 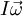 about the center of mass.
about the center of mass.
a. Suppose that the plane is inclined to the horizontal
at an angle θ in the earth's gravitational field. Show
that you can eliminate the constraint force to find an
equation for the center of mass alone and show that the
center of mass experiences an acceleration of 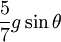 along
the 'downhill' direction in the plane. Hence, the
trajectries of this rolling sphere are parabolae.
along
the 'downhill' direction in the plane. Hence, the
trajectries of this rolling sphere are parabolae.
b. Now consider that the plane is not inclined, but is
rotating with angular velocity 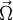 about the vertical
axis. The most important modification to the
calculation you have just done is that the condition
for rolling without slipping changes. Use the changed
condition in your previous analysis to show that the
free center of mass executes circular motion in the
horizontal inertial frame with frequency
about the vertical
axis. The most important modification to the
calculation you have just done is that the condition
for rolling without slipping changes. Use the changed
condition in your previous analysis to show that the
free center of mass executes circular motion in the
horizontal inertial frame with frequency 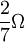 ! In other
words, the rolling sphere executes Lamor orbits, just
like a charged particle in a uniform magnetic field!
! In other
words, the rolling sphere executes Lamor orbits, just
like a charged particle in a uniform magnetic field!
For reference note that the moment of inertia of a
homogenous sphere is 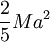 .
.
Taking the time derivative of the rolling without slipping condition:
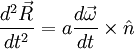
The only torque on the ball is the force to enforce rolling without friction:
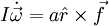
Rearranging:
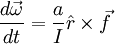
Plugging this in:
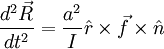
Since 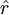 ,
so that
,
so that 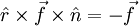 :
:
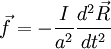
Writing the force equation in the downhill direction:
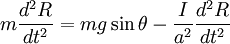
For a sphere 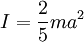 :
:
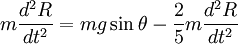
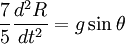
So we finally get:
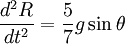
We change the condition for rolling without slipping to be:
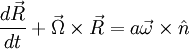
to take into account the motion of the ground. Taking the time derivative:
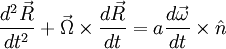
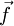 will be defined in the same way as before:
will be defined in the same way as before:
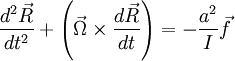
So that in the force equation:
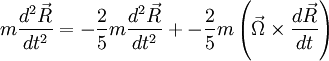
or:
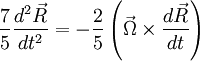
Since 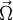 is perpendicular to the plane:
is perpendicular to the plane:
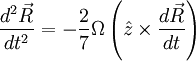
This is the equation of motion for a circle in the
plane, moving with frequency 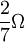 !
!
This page was recovered in October 2009 from the Plasmagicians page on Prelim_M03_Mech2 dated 23:15, 1 January 2006.












