Warning: jsMath requires JavaScript to process the mathematics on this page.
If your browser supports JavaScript, be sure it is enabled.

CM M05 1

From QED

< PlasmaWiki | Prelims(Link to this page as [[PlasmaWiki/Prelims/CM M05 1]])

Jump to: navigation, search

Sometimes it is required to reduce the influence of vertical floor vibration on experimental setups. To accomplish this, the experimental apparatus (of mass $M$ ) is mounted on gas-filled pistons (which have face area $A$ and equilibrium volume $V 0$ ). The gas pressure in the cylinder is much larger than atmospheric pressure. The pistons are typically equipped with a mechanism to damned their oscillations (by immersing part of the piston in oil), so that there is a retarding force, $- v M / τ$ , where $v$ is the velocity of the piston in the cylinder and $τ$ is a characteristic damping time.

- a) Ignoring damping ( 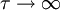$\tau \rightarrow \infty$ ), determine the resonance frequency $ω 0$ of the system for small vibrations. Explain whether any changes in state of the gas are more nearly isothermal or adiabatic.

- b) Characterize the performance of this vibration-isolation system as a function of frequency by calculating it's transmission coefficient, i.e. the ratio of the vibration amplitude of the apparatus to a small vibration amplitude of the floor. Include any phase shifts and express your answer in terms of $ω 0$ and the damping time $τ$ . For which frequency range do you expect this system to be useful for isolating the vibrations of the floor?

- c) How should the system parameters be chosen to provide as much vibration isolation as possible, subject to the constraint that a sudden displacement in the floor produces no oscillations in the system?

It is easy to get stuck on this problem. The first major issue is that it is not at all clear whether the system is more isothermal or adiabatic -- you can come up with heuristic arguments, but it's difficult to work on something you don't really believe in. In fact, the problem is underspecified: one can simply make an adiabatic piston by insulating it, and one may also make an isothermal piston by making it very tall and thermally conductive. We assume that the state equation for the system maybe be written as $p V γ = c o n s t a n t$ .

The next issue is that, for a steady state, the system appears to actually amplify movement, countering intuition (isolation systems are supposed to isolate, damn it!). On a closer inspection, it is not so crazy -- in the limit we use the system is like a mass on a damped spring, and it is easy to see that the steady state for such a system will lead to larger oscillations. It is not such a bad isolation system either -- luckily the homogenous part is nice to us and decays.

After these issues are dealt with, the last part is fairly straightforward -- a critically damped system is the best which doesn't allow oscillations from a sudden displacement.

The problem is underspecified, though from experience we guess that an adiabatic piston is more typically seen. We assume that the system obeys a power law $p V γ = c o n s t a n t$ . Then 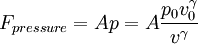$F_{pressure} = A p = A \frac{p_0 v_0^\gamma}{v^\gamma}$ , and $F g = - M g$ .

F t o t = F p r e s s u r e + F g, F 0 = A p 0 - M g

Implying

$F_{tot} = \frac{Mg(\frac{v_0}{A})^\gamma}{(\frac{v}{A})^\gamma} - Mg = \frac{Mg y_0}{y^\gamma} - Mg = Mg \left[{(\frac{y_0}{y})^\gamma - 1}\right]$ $\ddot{y} = g \left[{(\frac{y_0}{y})^\gamma - 1}\right]$

Expanding around 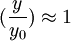$(\frac{y}{y_0}) \approx 1$ :

$\ddot{y} = g \left[{- \gamma \left({\frac{y}{y_0} - 1}\right) + O\left({(\frac{y}{y_0} - 1)^2}\right)}\right]$

For small oscillations

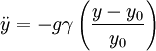
$\ddot{y} = - g \gamma \left({\frac{y - y_0}{y_0}}\right)$

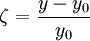Defining $\zeta = \frac{y - y_0}{y_0}$ , we have

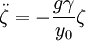
$\ddot{\zeta} = - \frac{g \gamma}{y_0} \zeta$

So the resonance frequency is 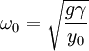$\omega_0 = \sqrt{\frac{g \gamma}{y_0} }$

Here, the pressure is given by the distance from the floor $(y')$ to the table $(y)$ .

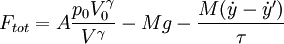
$F_{tot} = A \frac{p_0 V_0^\gamma}{V^\gamma} - Mg - \frac{M(\dot{y} - \dot{y}')}{\tau}$ $F_{tot} = (A p_0) \frac{\left[{A (y_0 -y_0')}\right]^\gamma}{\left[{A (y - y')}\right]^\gamma} - Mg - \frac{M(\dot{y} - \dot{y}')}{\tau}$ $F_{tot} = (Mg) \frac{y_0^\gamma}{\left[{y - y'}\right]^\gamma} - Mg - \frac{M(\dot{y} - \dot{y}')}{\tau}$ $\ddot{y} = g \frac{y_0^\gamma}{\left[{y - y'}\right]^\gamma} - g - \frac{(\dot{y} - \dot{y}')}{\tau}$

Expand the first term around $\frac{\left[{y - y'}\right]^\gamma}{y_0^\gamma} \approx 1$

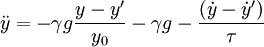
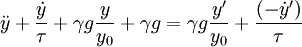
$\ddot{y} = g \left[{-\gamma \left({\frac{ y - y'}{y_0} - 1}\right) + O\left({\left({\frac{y - y'}{y_0} - 1}\right)^2}\right) }\right] - \frac{(\dot{y} - \dot{y}')}{\tau}$ $\ddot{y} = - \gamma g \frac{ y - y'}{y_0} - \gamma g - \frac{(\dot{y} - \dot{y}')}{\tau}$ $\ddot{y} + \frac{\dot{y}}{\tau} + \gamma g \frac{y}{y_0} + \gamma g = \gamma g \frac{y'}{y_0} + \frac{(- \dot{y}')}{\tau}$

Defining, for our convenience 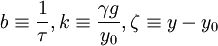$b \equiv \frac{1}{\tau}, k \equiv \frac{\gamma g}{y_0}, \zeta \equiv y - y_0$

Then 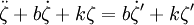$\ddot{\zeta} + b \dot{\zeta} + k \zeta = b \dot{\zeta}' + k \zeta'$

Assuming a sinusoidal motion in $ζ',ζ' = A sinω t$ . Then

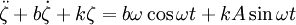
$\ddot{\zeta} + b \dot{\zeta} + k \zeta = b \omega \cos{\omega t} + k A \sin{\omega t}$

By the operator method (or experience) we see that the particular solution is of the form $ζ = C 1 cosω t + C 2 sinω t$ . Plugging in to the left side:

$\ddot{\zeta} + b \dot{\zeta} + k \zeta = \left[{(k - \omega^2) C_1 + b \omega C_2}\right] \cos{\omega t} + \left[{(k - \omega^2) C_2 - b \omega C_1}\right] \sin{\omega t}$

I translate both into the form $M 1 / 2 sin(ω t - φ 1 / 2)$ :

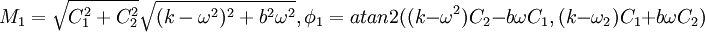
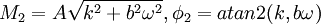
$M_1 = \sqrt{C_1^2 + C_2^2} \sqrt{(k-\omega^2)^2 + b^2 \omega^2}, \phi_1 = atan2 ((k - \omega^2) C_2 - b \omega C_1, (k - \omega_2) C_1 + b \omega C_2)$ $M_2 = A \sqrt{k^2 + b^2 \omega^2}, \phi_2 = atan2 (k,b\omega)$

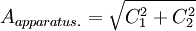$A_{apparatus.} = \sqrt{C_1^2 + C_2^2}$ is the vibration amplitude of the apparatus. Thus the gain is

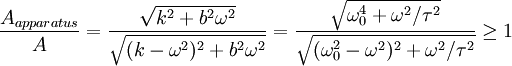
$\frac{A_{apparatus}}{A} = \frac{\sqrt{k^2 + b^2 \omega^2}}{\sqrt{(k-\omega^2)^2 + b^2 \omega^2}} = \frac{\sqrt{\omega_0^4 + \omega^2/\tau^2}}{\sqrt{(\omega_0^2-\omega^2)^2 + \omega^2 / \tau^2}} \geq 1$

At first glance this would seem to imply that the system is completely useless for damping -- luckily this is not so, as this is only the response to a steady state oscillation.

Equating the phases means equating the ratios of the arguments, thus

$\left[{(k - \omega^2) b \omega - k b \omega}\right] C_2 = \left[{k(k - \omega^2) + b^2 \omega^2}\right] C_1$

and since the floor is defined to have a shift of zero, the phase shift is

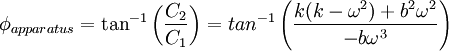
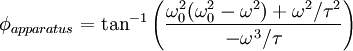
$\phi_{apparatus} = \tan^{-1}\left({\frac{C_2}{C_1}}\right) = tan^{-1}\left({\frac{k(k - \omega^2) + b^2 \omega^2}{- b \omega^3}}\right)$ $\phi_{apparatus} = \tan^{-1}\left({\frac{\omega_0^2(\omega_0^2 - \omega^2) + \omega^2/\tau^2}{- \omega^3 / \tau}}\right)$

The system will work reasonably well for frequency ranges far from $ω 0$ , where only a high damping constant will save you from wild oscillations!

The homogeneous equation is the familiar damped harmonic oscillator. From experience (and it is easy to show mathematically), transients are damped most quickly by critically damped devices (ie: where $1 / t a u = 2ω 0$ ), which will not oscillate due to sudden displacements. This system will do very well against transient effects. To deal with constant floor oscillations, a lower $τ$ may be required. Realistically constant oscillations are not handles at all well by this system -- it is better to think of something more clever, like say having a limited flow valve in the piston so that it does not actually increase the pressure by much when a floor oscillation occurs.

This page was recovered in October 2009 from the Plasmagicians page on Prelim_M05_Mech1 dated 02:21, 22 November 2006.

Retrieved from "https://qed.princeton.edu/main/PlasmaWiki/Prelims/CM_M05_1"

Category: Plasma Physics Completed Problems