Warning: jsMath requires JavaScript to process the mathematics on this page.
If your browser supports JavaScript, be sure it is enabled.

EM M00 1

From QED

< PlasmaWiki | Prelims(Link to this page as [[PlasmaWiki/Prelims/EM M00 1]])

Jump to: navigation, search

Suppose we have the plane wave in the conductor:

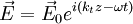
$\vec{E}=\vec{E}_{0}e^{i(k_{t}z-\omega t)}$

We take Maxwell's equations:

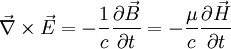
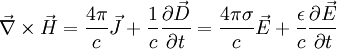
$\vec{\nabla}\times\vec{E}=-\frac{1}{c}\frac{\partial\vec{B}}{\partial t}=-\frac{\mu}{c}\frac{\partial\vec{H}}{\partial t}$ $\vec{\nabla}\times\vec{H}=\frac{4\pi}{c}\vec{J}+\frac{1}{c}\frac{\partial\vec{D}}{\partial t}=\frac{4\pi\sigma}{c}\vec{E}+\frac{\epsilon}{c}\frac{\partial\vec{E}}{\partial t}$

where we used the constituitive relations 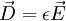$\vec{D}=\epsilon\vec{E}$ . Taking the curl of the first equation and using our vector relation, we get the wave equation:

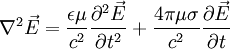
$\nabla^{2}\vec{E}=\frac{\epsilon\mu}{c^{2}}\frac{\partial^{2}\vec{E}}{\partial t^{2}}+\frac{4\pi\mu\sigma}{c^{2}}\frac{\partial\vec{E}}{\partial t}$

So:

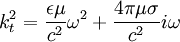
$k_{t}^{2}=\frac{\epsilon\mu}{c^{2}}\omega^{2}+\frac{4\pi\mu\sigma}{c^{2}}i\omega$

Or:

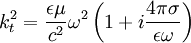
$k_{t}^{2}=\frac{\epsilon\mu}{c^{2}}\omega^{2}\left(1+i\frac{4\pi\sigma}{\epsilon\omega}\right)$

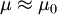Since $\mu\approx\mu_{0}$ :

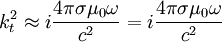
$k_{t}^{2}\approx i\frac{4\pi\sigma\mu_{0}\omega}{c^{2}}=i\frac{4\pi\sigma\mu_{0}\omega}{c^{2}}$

So:

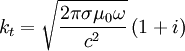
$k_{t}=\sqrt{\frac{2\pi\sigma\mu_{0}\omega}{c^{2}}}\left(1+i\right)$

We recognize the skin depth:

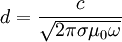
$d=\frac{c}{\sqrt{2\pi\sigma\mu_{0}\omega}}$

Yielding:

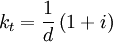
$k_{t}=\frac{1}{d}\left(1+i\right)$

We know the incoming $k i = ω / c$ . We must also have continuity across the boundary:

k i sinθ i = k t sinθ t

So that:

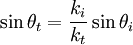
$\sin\theta_{t}=\frac{k_{i}}{k_{t}}\sin\theta_{i}$

Plugging in:

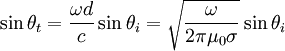
$\sin\theta_{t}=\frac{\omega d}{c}\sin\theta_{i}=\sqrt{\frac{\omega}{2\pi\mu_{0}\sigma}}\sin\theta_{i}$

Since we have a good conductor, this is 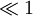$\ll1$ , and so we can write:

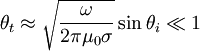
$\theta_{t}\approx\sqrt{\frac{\omega}{2\pi\mu_{0}\sigma}}\sin\theta_{i}\ll1$

So using 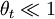$\theta_{t}\ll1$ we can expand:

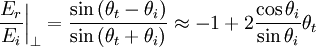
$\left.\frac{E_{r}}{E_{i}}\right|_{\perp}=\frac{\sin\left(\theta_{t}-\theta_{i}\right)}{\sin\left(\theta_{t}+\theta_{i}\right)}\approx-1+2\frac{\cos\theta_{i}}{\sin\theta_{i}}\theta_{t}$

And plugging in for $θ t$ :

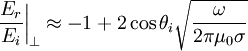
$\left.\frac{E_{r}}{E_{i}}\right|_{\perp}\approx-1+2\cos\theta_{i}\sqrt{\frac{\omega}{2\pi\mu_{0}\sigma}}$

So:

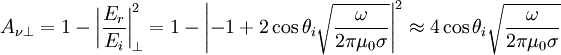
$A_{\nu\perp}=1-\left|\frac{E_{r}}{E_{i}}\right|_{\perp}^{2}=1-\left|-1+2\cos\theta_{i}\sqrt{\frac{\omega}{2\pi\mu_{0}\sigma}}\right|^{2}\approx4\cos\theta_{i}\sqrt{\frac{\omega}{2\pi\mu_{0}\sigma}}$

Where we discarded the higher order term in the small value. And so, using $ω = ν / 2π$ :

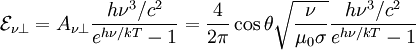
$\mathcal{E}_{\nu\perp}=A_{\nu\perp}\frac{h\nu^{3}/c^{2}}{e^{h\nu/kT}-1}=\frac{4}{2\pi}\cos\theta\sqrt{\frac{\nu}{\mu_{0}\sigma}}\frac{h\nu^{3}/c^{2}}{e^{h\nu/kT}-1}$

We simply need to expand the other fraction:

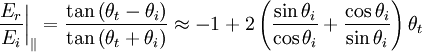
$\left.\frac{E_{r}}{E_{i}}\right|_{\|}=\frac{\tan\left(\theta_{t}-\theta_{i}\right)}{\tan\left(\theta_{t}+\theta_{i}\right)}\approx-1+2\left(\frac{\sin\theta_{i}}{\cos\theta_{i}}+\frac{\cos\theta_{i}}{\sin\theta_{i}}\right)\theta_{t}$

Plugging in:

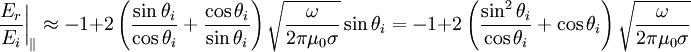
$\left.\frac{E_{r}}{E_{i}}\right|_{\|}\approx-1+2\left(\frac{\sin\theta_{i}}{\cos\theta_{i}}+\frac{\cos\theta_{i}}{\sin\theta_{i}}\right)\sqrt{\frac{\omega}{2\pi\mu_{0}\sigma}}\sin\theta_{i}=-1+2\left(\frac{\sin^{2}\theta_{i}}{\cos\theta_{i}}+\cos\theta_{i}\right)\sqrt{\frac{\omega}{2\pi\mu_{0}\sigma}}$

Which we can rewrite as:

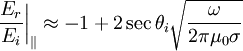
$\left.\frac{E_{r}}{E_{i}}\right|_{\|}\approx-1+2\sec\theta_{i}\sqrt{\frac{\omega}{2\pi\mu_{0}\sigma}}$

Which we can plug in for the absorption coefficient:

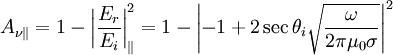
$A_{\nu\|}=1-\left|\frac{E_{r}}{E_{i}}\right|_{\|}^{2}=1-\left|-1+2\sec\theta_{i}\sqrt{\frac{\omega}{2\pi\mu_{0}\sigma}}\right|^{2}$

Where we keep the higher order term since $secθ i$ is unbounded. This gives us:

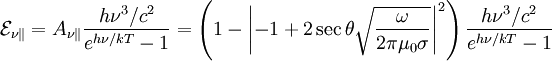
$\mathcal{E}_{\nu\|}=A_{\nu\|}\frac{h\nu^{3}/c^{2}}{e^{h\nu/kT}-1}=\left(1-\left|-1+2\sec\theta\sqrt{\frac{\omega}{2\pi\mu_{0}\sigma}}\right|^{2}\right)\frac{h\nu^{3}/c^{2}}{e^{h\nu/kT}-1}$

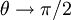As $\theta\rightarrow\pi/2$ , the polarization will be entirely parallel to the plane of emission. This is because the wave is caused by the motion of the electrons in the conductor, which cannot move out of the plane, and since EM radiation is transverse, the waves must be caused only by electron motion parallel to this plane.