EM M03 2
From QED
The 'method of images' allows us to solve many problems involving point charges and spherical conductors of various kinds. In this questions you are asked to derive and then use this method in some representative applications.
(a) Consider a charge Q placed at a distance R > a from the center of a sphere of radius a (for the moment, this is just a geometrical sphere, not a conductor or any other physical object). Show that is a certain charge of opposite sign is placed inside the sphere at the appropriate location then the spherical surface of radius a is a V = 0 equipotential surface. This result can be used in the following applications:
(b) A point charge Q is placed at a distance R > a from the center of a conducting sphere of radius a. Find the force exerted on the sphere if the total charge on the sphere is Q.
(c) Consider the distribution of the total charge Q on the surface of the sphere under the conditions just described. Find an equation for the distance R such that surface charge density of opposite sign to Q first appears somewhere of the sphere.
(d) Two perfectly conducting spheres of radius a are placed far apart (their centers are separated by 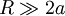 ) and kept at the same potential V0 (this condition could be enforced by connecting the sphere with a fine wire). What is the charge on each sphere, correct to first order in a / R?
) and kept at the same potential V0 (this condition could be enforced by connecting the sphere with a fine wire). What is the charge on each sphere, correct to first order in a / R?
(e) What is the charge on the two spheres correct to second order in a / R?
We can put the image charge at 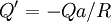 . Let us
take coordinates so that the charges are on the
. Let us
take coordinates so that the charges are on the  axis.
This gives the field:
axis.
This gives the field:
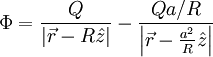
At 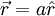 :
:
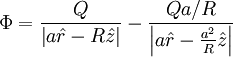
Simplifying the second term:
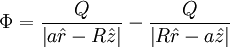
Or, using θ as the angle between 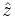 :
:
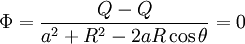
We put the image charge 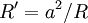 . To make the sphere have
total charge Q, we add charge:
. To make the sphere have
total charge Q, we add charge:
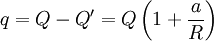
at the origin. The force will then be the force of the one charge on these two image charges:
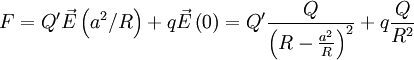
Plugging in:
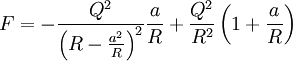
So that the total force is:
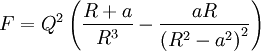
The surface density is given by:
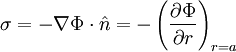
We have the potential:
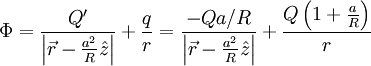
Which gives charge density at 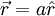 :
:
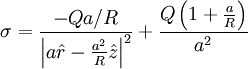
This is a minimum at 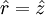 , and will have a negative value
just after it has a zero value:
, and will have a negative value
just after it has a zero value:
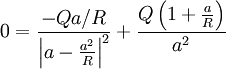
Rearranging:
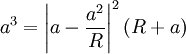
Let us put our four charges along the x-axis (two for the charge on the spheres, two for the image charges).
The potential due to the charge in the center of the sphere is
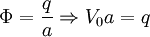
So put charge q at x=0, x=R. Then we get image charges
at x = a2 / R , x = R − a2 / R , with 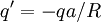 . So the total charge on one sphere is:
. So the total charge on one sphere is:
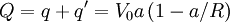
To the next order, we find the image charge due to the image charges. They will be at:
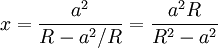
and 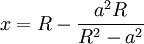 . They will have charge:
. They will have charge:
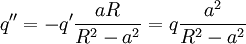
So that the total charge is:
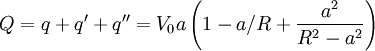
This page was recovered in October 2009 from the Plasmagicians page on Prelim_M03_EM2 dated 02:18, 13 August 2006.












