SM J97 1

From QED

< PlasmaWiki | Prelims(Link to this page as [[PlasmaWiki/Prelims/SM J97 1]])
Jump to: navigation, search

Atoms of spin S=1/2 are arranged on a simple-cubic lattice of lattice constant a. Nearest neighbor spins interact antiferromagnetically with a Heisenberg Hamiltonian:

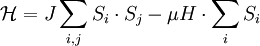
\mathcal{H}=J\sum_{i,j}S_{i}\cdot S_{j}-\mu H\cdot\sum_{i}S_{i}

where i and j are nearest neighbors.

Within the mean field approximation, calculate:

a. The Neel temperature TN below which the system is antiferromagnetically ordered

b. The magnetic susceptibility for 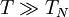T\gg T_{N}

Using the mean field approximation, we write the new Hamiltonian:

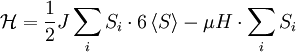
\mathcal{H}=\frac{1}{2}J\sum_{i}S_{i}\cdot6\left\langle S\right\rangle -\mu H\cdot\sum_{i}S_{i}

with the \frac{1}{2} to avoid double-counting and 6 for the number of neighbors. Moving out the sum:

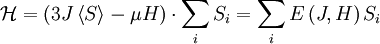
\mathcal{H}=\left(3J\left\langle S\right\rangle -\mu H\right)\cdot\sum_{i}S_{i}=\sum_{i}E\left(J,H\right)S_{i}

where we have defined E(J,H) for this to be true. Thus we can write the partition function:

Z_{1}=\sum_{S_{i}=-1,1}\exp\left[-\beta E\left(J,H\right)S_{i}\right]=2\cosh\left(\beta E\left(J,H\right)\right)

We can write the probability of a state:

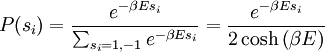
P(s_{i})=\frac{e^{-\beta Es_{i}}}{\sum_{s_{i}=1,-1}e^{-\beta Es_{i}}}=\frac{e^{-\beta Es_{i}}}{2\cosh\left(\beta E\right)}

And we thus find the expectation of the state:

\left\langle S\right\rangle =\sum_{i}\frac{s_{i}e^{-\beta Es_{i}}}{2\cosh\left(\beta E\right)}=-\tanh\left[\beta\left(3J\left\langle S\right\rangle -\mu H\right)\right]

This can only have a transition into being antiferromagnetically ordered (ie, have multiple solutions) if Failed to parse (syntax error): \frac{d}{d\langle S\rangle}RHS&gt;\frac{d}{d\langle S\rangle}LHS 

 somewhere. This gives  3βJ = 3J / kBT > 1 , which can be rearranged:

<math>T_{N}=\frac{3J}{k_{B}}</math>

We can write the magnetic susceptability:

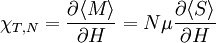
\chi_{T,N}=\frac{\partial\langle M\rangle}{\partial H}=N\mu\frac{\partial\langle S\rangle}{\partial H}

since M=N\mu S is just the aggregated moment. We know:

\langle S\rangle=-\tanh\left[\beta\left(3J\left\langle S\right\rangle -\mu H\right)\right]

and so:

\frac{\partial\langle S\rangle}{\partial H}=-\mathrm{sech}^{2}\left[\beta\left(3J\left\langle S\right\rangle -\mu H\right)\right]\beta\left(3J\frac{\partial\langle S\rangle}{\partial H}-\mu\right)

Solving for 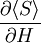\frac{\partial\langle S\rangle}{\partial H} :

\frac{\partial\langle S\rangle}{\partial H}=\frac{\mu\beta}{\cosh^{2}\left[\beta\left(3J\left\langle S\right\rangle -\mu H\right)\right]-3\beta J}

Plugging in:

\chi_{T,N}=\frac{N\mu^{2}\beta}{\cosh^{2}\left[\beta\left(3J\left\langle S\right\rangle -\mu H\right)\right]-3\beta J}

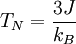As T_{N}=\frac{3J}{k_{B}} , we can write β = 1 / kBT = (TN / T) / 3J :

\chi_{T,N}=\frac{N\mu^{2}T_{N}/3JT}{\cosh^{2}\left[\frac{T_{N}}{T}\left(\left\langle S\right\rangle -\mu H/3J\right)\right]-T_{N}/T}

Noting that 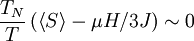\frac{T_{N}}{T}\left(\left\langle S\right\rangle -\mu H/3J\right)\sim0 . Using this and rearranging:

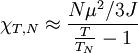
\chi_{T,N}\approx\frac{N\mu^{2}/3J}{\frac{T}{T_{N}}-1}

Since 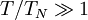T/T_{N}\gg1 and: 

<math>\chi_{T,N}\approx\frac{N\mu^{2}T_{N}}{3JT}</math>

This page was recovered in October 2009 from the Plasmagicians page on Prelim_J97_SMT1 dated 02:17, 13 August 2006.

Retrieved from "https://qed.princeton.edu/main/PlasmaWiki/Prelims/SM_J97_1"
Personal tools