Warning: jsMath requires JavaScript to process the mathematics on this page.
If your browser supports JavaScript, be sure it is enabled.

WavesBestiary

From QED

< PlasmaWiki(Link to this page as [[PlasmaWiki/WavesBestiary]])

Jump to: navigation, search

The Waves Bestiary

Sit in reverie, and watch the changing color of the waves that break upon the idle seashore of the mind

- Henry Wadsworth Longfellow

This page is intended to be a summary of the various types of waves encountered in plasma physics. It was originally created by Abe Fetterman, then redone and expanded by Craig Jacobson, and finally moved from LaTeX to the PlasmaWiki. Surely there are errors in this document. Please correct them as they are found. There also seem to be some errors with wiki formatting. Please correct those as well. All the equations are in cgs units because the source material for this is Waves in Plasmas by Stix.

Cold Plasma Waves (By ascending frequency)

Alfvén Hydromagnetic Waves

Here we assume 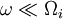$\omega\ll\Omega_{i}$ . There are two. One is the \emph{slow} or \emph{shear} or \emph{torsional} Alfvén wave:

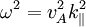
$\omega^{2}=v_{A}^{2}k_{\|}^{2}$

And the other is the \emph{fast} or \emph{compressional} Alfvén wave:

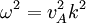
$\omega^{2}=v_{A}^{2}k^{2}$

Ion Cyclotron Waves

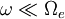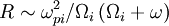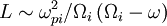The slow Alfvén wave is cutoff, and the dispersion relation is renamed the ion cyclotron wave when Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): \omega\sim\Omega_{i} . We assume $\omega\ll\Omega_{e}$ . One finds $R\sim\omega_{pi}^{2}/\Omega_{i}\left(\Omega_{i}+\omega\right)$ and $L\sim\omega_{pi}^{2}/\Omega_{i}\left(\Omega_{i}-\omega\right)$ . The dispersion relation is then (for both Alfvén waves, combined):

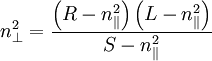
$n_{\perp}^{2}=\frac{\left(R-n_{\|}^{2}\right)\left(L-n_{\|}^{2}\right)}{S-n_{\|}^{2}}$

The Alfvén resonance occurs at 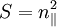$S=n_{\|}^{2}$ .

Lower Hybrid Waves

The lower hybrid wave may be derived using the electrostatic approximation in the lower hybrid frequency range Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): (\Omega_{i}\ll\omega\ll\Omega_{e}) . The X-mode is affected by the lower hybrid resonance, which occurs at Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): \omega_{LH}

defined by:

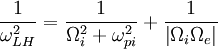
$\frac{1}{\omega_{LH}^{2}}=\frac{1}{\Omega_{i}^{2}+\omega_{pi}^{2}}+\frac{1}{\left|\Omega_{i}\Omega_{e}\right|}$

At the frequency 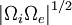$\left|\Omega_{i}\Omega_{e}\right|^{1/2}$ , the minor diameter of the electron trajectory is equal to the major diameter of the ion trajectory, and this is the source of the resonance.

Quasi-Transverse (QT) Waves

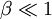This is a general term for electromagnetic waves propagating approximately perpendicular to the \emph{magnetic} field (counter to nomenclature), with Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): \omega\gg\Omega_{i},\omega_{pi} , $\beta\ll1$ . There are two QT modes. The QT-O mode is:

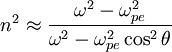
$n^{2}\approx\frac{\omega^{2}-\omega_{pe}^{2}}{\omega^{2}-\omega_{pe}^{2}\cos^{2}\theta}$

Then for perpendicular (Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): \theta=\pi/2 ) propagation, this wave corresponds to Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): n^{2}=P . The QT-X mode is:

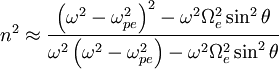
$n^{2}\approx\frac{\left(\omega^{2}-\omega_{pe}^{2}\right)^{2}-\omega^{2}\Omega_{e}^{2}\sin^{2}\theta}{\omega^{2}\left(\omega^{2}-\omega_{pe}^{2}\right)-\omega^{2}\Omega_{e}^{2}\sin^{2}\theta}$

For Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): \theta=\pi/2 , this wave corresponds to Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): n^{2}=RL/S .

Quasi-Longitudinal (QL) Waves (Electron Cyclotron and Whistler Waves)

This is a general term for electromagnetic waves propagating approximately parallel to the magnetic field (counter to nomenclature), with Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): \omega\gg\Omega_{i} , Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): \omega_{pi} , 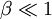$\beta\ll1$ . One may find:

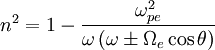
$n^{2}=1-\frac{\omega_{pe}^{2}}{\omega\left(\omega\pm\Omega_{e}\cos\theta\right)}$

Where the QL-R wave corresponds to the positive sign, and the QL-L wave corresponds to the negative sign. The QL-R wave is sometimes known as the whistler wave because the group velocity increases with frequency. The QL-R wave is sometimes also referred to as the electron cyclotron wave, due to the resonance at the electron cyclotron frequency.

Upper Hybrid Waves

The upper hybrid wave dispersion relation may be found by using the electrostatic approximation in this regime. The X-mode is affected by the upper hybrid resonance, Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): \omega_{UH}

defined by:

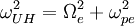
$\omega_{UH}^{2}=\Omega_{e}^{2}+\omega_{pe}^{2}$

This may be described as the frequency at which electrons on a flux tube boundary would oscillate if they were all simultaneously displaced outward.

Warm plasma waves

Ion Acoustic Wave

The ion acoustic wave is analagous to the cold plasma Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): P=0

wave.

Therefore, we set Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): \epsilon_{zz}=0 , and find:

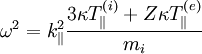
$\omega^{2}=k_{\|}^{2}\frac{3\kappa T_{\|}^{\left(i\right)}+Z\kappa T_{\|}^{\left(e\right)}}{m_{i}}$

Here $κ$ is Boltzmann's constant. These will be strongly damped by Landau damping unless 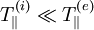$T_{\|}^{\left(i\right)}\ll T_{\|}^{\left(e\right)}$ , which then gives the relation Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): \omega^{2}=k_{\|}^{2}c_{s}^{2} .

Electrostatic Ion Cyclotron Wave

If we use the electrostatic approximation, and assume Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): \omega\ll\Omega_{e}<math>, allowing finite <math>k_{x}

and including warm plasma effects, we find

the dispersion relation:

Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): \omega^{2}=\Omega_{i}^{2}+k_{x}^{2}c_{s}^{2}

Lower-Hybrid Waves

The lower hybrid waves assume Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): \Omega_{i}<\omega\ll\Omega_{e} . If we include warm plasma effects and density gradients, we get the dispersion relation:

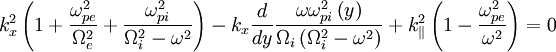
$k_{x}^{2}\left(1+\frac{\omega_{pe}^{2}}{\Omega_{e}^{2}}+\frac{\omega_{pi}^{2}}{\Omega_{i}^{2}-\omega^{2}}\right)-k_{x}\frac{d}{dy}\frac{\omega\omega_{pi}^{2}\left(y\right)}{\Omega_{i}\left(\Omega_{i}^{2}-\omega^{2}\right)}+k_{\|}^{2}\left(1-\frac{\omega_{pe}^{2}}{\omega^{2}}\right)=0$

Drift Waves

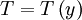Drift waves are low frequency electrostatic waves. They arise in inhomogenous (Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): n=n ), $T=T\left(y\right)$ ) plasmas with finite parallel electron temperature. The two possibilities are adiabatic:

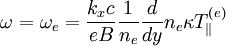
$\omega=\omega_{e}=\frac{k_{x}c}{eB}\frac{1}{n_{e}}\frac{d}{dy}n_{e}\kappa T_{\|}^{\left(e\right)}$

And isothermal:

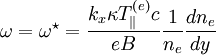
$\omega=\omega^{\star}=\frac{k_{x}\kappa T_{\|}^{\left(e\right)}c}{eB}\frac{1}{n_{e}}\frac{dn_{e}}{dy}$

Where the isothermal law is usually the relevant one (it is relevant assuming 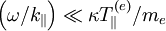$\left(\omega/k_{\|}\right)\ll\kappa T_{\|}^{\left(e\right)}/m_{e}$ ).

Hot Plasma Waves

Ion Cyclotron Waves

In the hot plasma regime, the ion cyclotron wave dispersion relation (also describing the shear Alfvén wave) may be written as:

$n_{\|}^{2}=1-\frac{\omega_{pi}^{2}}{\omega\Omega_{i}}+\left[\frac{\omega_{p}^{2}}{\omega k_{\|}w}Z_{0}\left(\zeta_{1}\right)\right]_{i}$

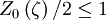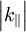Note that since $Z_{0}\left(\zeta\right)/2\leq1$ for real $ζ$ , there is a maximum value for $\left|k_{\|}\right|$ .

Magnetosonic Waves

These waves correspond to the fast Alfvén wave, so 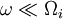$\omega\ll\Omega_{i}$ . The dispersion relation is:

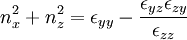
$n_{x}^{2}+n_{z}^{2}=\epsilon_{yy}-\frac{\epsilon_{yz}\epsilon_{zy}}{\epsilon_{zz}}$

Electron Cyclotron Waves

In the hot plasma regime, the electron cyclotron wave (or QL-L) dispersion relation may be written as:

$n_{\|}^{2}=1-\frac{\omega_{pi}^{2}}{\omega^{2}}+\left[\frac{\omega_{p}^{2}}{\omega k_{\|}w}Z_{0}\left(\zeta_{-1}\right)\right]_{e}$

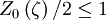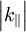Note that since $Z_{0}\left(\zeta\right)/2\leq1$ for real $ζ$ , there is a maximum value for $\left|k_{\|}\right|$ .

Nonresonant Perpendicular Waves

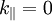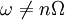Assuming $k_{\|}=0$ and $\omega\neq n\Omega$ , we find two dispersion relations corresponding to QT-O waves (Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): n^{2}=P ):

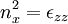
$n_{x}^{2}=\epsilon_{zz}$

which are electromagnetic, and QT-X waves 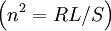$\left(n^{2}=RL/S\right)$ :

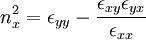
$n_{x}^{2}=\epsilon_{yy}-\frac{\epsilon_{xy}\epsilon_{yx}}{\epsilon_{xx}}$

These waves are approximately electrostatic. \emph{Bernstein waves} are a subclass of these QT-X waves.

Bernstein Waves}

To derive these waves, it is necessary that 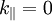$k_{\|}=0$ and Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): V=0 . Bernstein waves are electrostatic waves that are cut off near (just below) the cyclotron harmonics. The dispersion relation is given by:

Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): \epsilon_{xx}=1-\sum_{s}\frac{4\pi n_{s}m_{s}c^{2}}{B_{0}^{2}}\frac{\alpha\left(q_{s},\lambda_{s}\right)}{\lambda_{s}}=0,\;\alpha\left(q,\lambda\right)=2\sum_{n=1}^{\infty}e^{-\lambda}I_{n}\left(\lambda\right)\frac{n^{2}}{q^{2}-n^{2}}

with Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): q=\omega/\Omega . For frequencies well above Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): \Omega_{i} , we have approximately the \emph{electron Bernstein mode}, with dispersion relation:

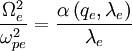
$\frac{\Omega_{e}^{2}}{\omega_{pe}^{2}}=\frac{\alpha\left(q_{e},\lambda_{e}\right)}{\lambda_{e}}$

while for frequencies well below Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): \Omega_{e} , the wave describes an \emph{ion Bernstein mode}, with dispersion relation:

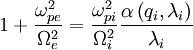
$1+\frac{\omega_{pe}^{2}}{\Omega_{e}^{2}}=\frac{\omega_{pi}^{2}}{\Omega_{i}^{2}}\frac{\alpha\left(q_{i},\lambda_{i}\right)}{\lambda_{i}}$

Instabilities

Landau Damping

Landau damping occurs for Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): \omega\sim vt

for some species. It is

valid in the collisional regime where Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): \nu_{coll}\tau_{osc}>1

and

Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): k_{\|}\lambda_{mfp}<1 . The collision time is greater than the oscillation time in the electrostatic well (therefore, particles can be considered uncorrelated). The relevant wavelength must be less than the mean free path (so that the plasma is not considered truly collisional). The dispersion relation is:

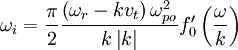
$\omega_{i}=\frac{\pi}{2}\frac{\left(\omega_{r}-kv_{t}\right)\omega_{po}^{2}}{k\left|k\right|}f_{0}^{\prime}\left(\frac{\omega}{k}\right)$

Assuming 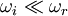$\omega_{i}\ll\omega_{r}$ .

Two-Stream Instability

This instability occurs for two-peaked energy distributions, beam species, or fast particles. The condition for instability is that:

Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): \frac{\mathbf{k}\cdot\left(\mathbf{v}_{1}-\mathbf{v}_{2}\right)}{2\omega_{po}}<1

Where 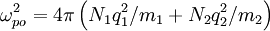$\omega_{po}^{2}=4\pi\left(N_{1}q_{1}^{2}/m_{1}+N_{2}q_{2}^{2}/m_{2}\right)$ . The fastest growing mode corresponds to Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): x^{2}=3/8

and has growth

rate:

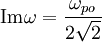
$\mathrm{Im}\omega=\frac{\omega_{po}}{2\sqrt{2}}$

Rayleigh-Taylor Instability

This instability occurs when the magnetic field, acting as a light fluid, must accelerate a heavy fluid, the plasma. This an the instability that grows, for example, in bad curvature regions. The dispersion relation in the case that 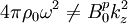$4\pi\rho_{0}\omega^{2}\neq B_{0}^{p}k_{z}^{2}$ ( $p$ superscripts indicate values in the plasma, $v$ superscripts indicate values in the vacuum):

$\omega^{2}=\frac{1}{4\pi\rho_{0}}\left[\left(\mathbf{B}_{0}^{p}\cdot\mathbf{k}\right)^{2}+\left(\mathbf{B}_{0}^{v}\cdot\mathbf{k}\right)^{2}\right]-g\left(k_{x}^{2}+k_{z}^{2}\right)^{1/2}$

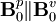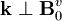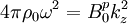where $\mathbf{B}_{0}^{p}\|\mathbf{B}_{0}^{v}$ , so that this will be unstable anywhere $\mathbf{k}\perp\mathbf{B}_{0}^{v}$ . The case that $4\pi\rho_{0}\omega^{2}=B_{0}^{p}k_{z}^{2}$ is stable and damped in Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): k_{y} .

Transit-Time Damping

Transit-time damping is the magnetic analog to Landau damping. It comes from the interaction of the magnetic moment of a gyrating particle, \textgreek{m}, with a parallel magnetic field gradient. Because the resonance condition is the same as the Landau damping (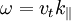 $\omega=v_{t}k_{\|}$ ), there may be either constructive or destructive coherence between the two processes.

Fire-Hose Instability

The fire-hose instability arises from the hot plasma shear Alfvén wave. The instability condition is that:

Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): \beta_{\|}>\beta_{\perp}+2

with 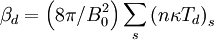$\beta_{d}=\left(8\pi/B_{0}^{2}\right)\sum_{s}\left(n\kappa T_{d}\right)_{s}$ . One may think of it as:

Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): p_{\|}>p_{\perp}+\frac{B_{0}^{2}}{4\pi}

The instability occurs when deviations in the field line direction cause the parallel pressure to oppose the perpendicular pressure. If it is stronger, it stretches the field lines and the instability grows.

Magnetosonic Instability

The magnetosonic instability arises from the magnetosonic move (compressional Alfvén wave). In the case that Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): \left(T_{\parallel}/T_{\perp}\right)_{i}=\left(T_{\|}/T_{\perp}\right)_{e} , the instability condition is that:

Failed to parse (PNG conversion failed; check for correct installation of latex, dvips, gs, and convert): \frac{\beta_\perp^{2}}{\beta_\parallel} > 1+\beta_\perp

This is a pressure-anisotropy driven instability.

Retrieved from "https://qed.princeton.edu/main/PlasmaWiki/WavesBestiary"

Category: Plasma Waves

WavesBestiary

From QED

Contents

Cold Plasma Waves (By ascending frequency)

Alfvén Hydromagnetic Waves

Ion Cyclotron Waves

Lower Hybrid Waves

Quasi-Transverse (QT) Waves

Quasi-Longitudinal (QL) Waves (Electron Cyclotron and Whistler Waves)

Upper Hybrid Waves

Warm plasma waves

Ion Acoustic Wave

Electrostatic Ion Cyclotron Wave

Lower-Hybrid Waves

Drift Waves

Hot Plasma Waves

Ion Cyclotron Waves

Magnetosonic Waves

Electron Cyclotron Waves

Nonresonant Perpendicular Waves

Bernstein Waves}

Instabilities

Landau Damping

Two-Stream Instability

Rayleigh-Taylor Instability

Transit-Time Damping

Fire-Hose Instability

Magnetosonic Instability

Views

Personal tools

Navigation

princeton

Search

Toolbox

WavesBestiary

From QED

Contents

Cold Plasma Waves (By ascending frequency)

Alfvén Hydromagnetic Waves

Ion Cyclotron Waves

Lower Hybrid Waves

Quasi-Transverse (QT) Waves

Quasi-Longitudinal (QL) Waves (Electron Cyclotron and Whistler Waves)

Upper Hybrid Waves

Warm plasma waves

Ion Acoustic Wave

Electrostatic Ion Cyclotron Wave

Lower-Hybrid Waves

Drift Waves

Hot Plasma Waves

Ion Cyclotron Waves

Magnetosonic Waves

Electron Cyclotron Waves

Nonresonant Perpendicular Waves

Bernstein Waves}

Instabilities

Landau Damping

Two-Stream Instability

Rayleigh-Taylor Instability

Transit-Time Damping

Fire-Hose Instability

Magnetosonic Instability

Views

Personal tools

Navigation

princeton

Search

Toolbox

Tag This!