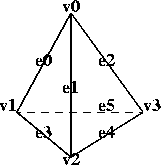
On the illustration at the left, the vertices are numbered v0 through v4, and the edges, e0 through e5. The faces are numbered as shown in the following table:
The way slice3 works depends strongly on a standard ordering of the nodes, edges, and faces of mesh cells. In this section we shall delineate the standard ordering used. This ordering is encapsulated in various tables contained in slice3.py and arrayfnsmodule.c. The maintainer of this code must have an understanding of this order.
On the illustration at the left, the vertices are numbered v0 through v4, and the edges, e0 through e5. The faces are numbered as shown in the following table:
face number | edges on face |
|---|---|
face number | edges on face |
|---|---|
face number | edges |
|---|---|
face number | edges |
|---|---|
Suppose we have a regular rectangular mesh whose cell dimensions are ni - 1 by nj - 1 by nk - 1 (and thus the vertex array is ni by nj by nk). The total number of cells is
and the cells are numbered from 0 to ncells - 1 according to the following scheme. Suppose that (i, j, k) are the maximum subscripts of the eight vertices of a cell numbered N in our scheme. Then the number of the cell with maximum vertex subscripts (i, j, k + 1) will be N + 1; the number of the cell with maximum vertex subscripts(i, j + 1, k) will be N + nk; and the number of the cell with maximum vertex subscripts(i + 1, j, k) will be N + nj * nk. Thus each triple of subscripts (i, j, k), where none of the three is zero, uniquely determines a cell number, and cell numbers run consecutively as we increment the subscripts through their ranges (starting with 1) in row major order. Similarly, we can number the vertices from 0 through ni * nj * nk - 1 by numbering them consecutively as we increment the subscripts through their ranges (starting with 0) in row major order.
This leads for the following scheme for computing the vertex numbers for all eight of the vertices of a cell, given the cell number. First, construct the scalar
Then, add this scalar to each element of the 2 x 2 x 2 array
The result is a 2 x 2 x 2 array of the vertex numbers of the vertices of the cell. Given that the arrays of vertex coordinates are stored in row major order, then if we ravel them (i. e., flatten them out), flatten the above array of vertex numbers, extract precisely those eight coordinates from each coordinate array, and then reshape them to 2 x 2 x 2, then we have the coordinates of the vertices of the cell under consideration.
The function to_corners3 does this calculation for an arbitrary list of cell numbers (see 8.15 "Find Corner Indices of List of Cells: to_corners3"8.15 "Find Corner Indices of List of Cells: to_corners3"). The function slice3 calls to_corners3 with a list of cells which are cut by a plane or isosurface in a rectangular mesh in order to determine the coordinates of their vertices, the final goal being to find the points at which the edges are cut by the plane or isosurface. These edge points are then connected in a systematic way using (among other things) the numbering schemes described previously, in order to yield the polygonal sections through cells made by the plane or isosurface.
Recall the calling sequence of slice3 (see see Section 7.4.2 "slice3: Plane and Isosurface Slices of a 3-D mesh" on page 65):
The important arguments are m3, a mesh specification which was returned by an earlier call of mesh3 (see 7.3.2 "Creating a mesh3 argument"); fslice (which specifies either the name of a slicing function, a slicing plane in plane3 format (see Section 7.3.1 "Creating a Plane" on page 61), or the number of the function defined on the mesh with respect to which an isosurface is to be computed); fcolor, which (if None) specifies that the section is to be shaded, or (if a function) gives a set of values on the the cells specified to it when slice3 calls it; value, which in the case of an isosurface specifies the value of the function doing the slicing; and node, which if nonzero and color is calculated, says to return node-centered rather than cell-centered values.
One of the first things that slice3 does is to call iterator3 with m3 as argument, which in turn calls the appropriate iterator for the particular type of mesh. (Recall that m3 contains names of appropriate functions to call for this mesh.) The purpose of iterator3 is to ``chunk'' up the mesh into manageable pieces; the main loop in slice3 calls iterator3 repeatedly until it finally returns None, signalling that the entire mesh has been processed. The details of both types of iterator are straightforward and can be had by inspecting the source code. One thing to bear in mind is that in the case of an unstructured mesh, iterator3 is guaranteed to return a chunk which consists of only one type of cell.
Why ``chunk'' up the mesh? The creators of the Yorick version of slice3, Langer and Munro, did so in order to avoid the possibility of creating very large temporaries and thus, perhaps, having memory problems. It seemed to us judicious to do the same thing.
The first thing done inside the slice3 main loop is to call the appropriate slicing function. Two functions are supplied in slice3.py. Their calling sequences and descriptions are as follows:
_isosurface_slicer (m3, chunk, iso_index, _value)
an isosurface slicer brings back a list [vals, None] where vals is simply an array of the values of the iso_indexth mesh function on the vertices of the specified chunk, or (in the unstructured case) a triple, consisting of the array of values, an array of relative cell numbers in the chunk, and an offset to add to the preceding to get absolute cell numbers.
_plane_slicer (m3, chunk, normal, projection)
In the case of a plane slice, this returns a list [vals, _xyz3] (or [ [vals, clist, cell_offset], _xyz3] in the irregular case) where _xyz3 is the array of vertices of the chunk. _xyz3 is ncells by 3 by something (in the irregular case), ncells by 3 by 2 by 2 by 2 in the regular case,and 3 by ni by nj by nk otherwise. vals will be the values of the projections of the corresponding vertex on the normal to the plane, positive if in front, and negative if in back.
In addition, the user may supply a slicing function; if so, its calling sequence must be of the form
and it must return something resembling the returned values above. If the m3 mesh is totally unstructured, the chunk should be arranged so that fslice returns an ncells-by-2-by-2-by-2 [hex case] (or ncells-by-3-by-2 [prism] or ncells-by-5 [pyramid] or ncells-by-4 [tet]) array of vertex values of the slicing function. Note that a chunk of an irregular mesh always consists of just one kind of cell. On the other hand, if the mesh vertices are arranged in a rectangular grid (or a few patches of rectangular grids), the chunk should be the far less redundant rectangular patch.
The critical cells are those cells (if any) which are cut by the slicing plane or isosurface. There are precisely those cells on the vertices of which the vals returned by the slicing function changes sign. For cells of one of the four types present in an unstructured mesh, one adds up the number of vertices on which vals is negative. If this is a positive number and also less than the number of vertices for that cell type, then the cell is critical. In the structured case, vals is ni by nj by nk. To the array which is 1 where vals is negative and 0 elsewhere, we apply the zcen_ (see page 101) function along each of its three dimensions. The result is an array ni - 1 by nj - 1 by nk - 1 of values defined on each cell which can be one of the nine values 0., .125, .25, .375, .5, .625, .75, .875, 1.0. Those cells where the value is strictly between the two end values are critical. Thus we form clist, which is an array of absolute cell numbers of the critical cells.
If clist is not empty, then we extract the coordinates of the critical cells, the data values at these points, and (if appropriate) the colors of the cells. In the case of a structured mesh, we use the to_corners3 function discussed earlier (see page 109) to convert cell numbers to node numbers, in order to get the node coordinates and data. We append a list of this to our list of results (appending [None, None, None, None] if clist is empty) and then continue iterating.
Once this loop completes, there is another for loop which loops through each type of cell (structured meshes are lumped under hex cells) present in the mesh, putting together the ``chunks'' of results if necessary. It then calls find_mask (page 105), which returns a mask array ncells * ne long (ncells is the total number of cells of this type, ne the number of edges on a cell) which contains 1's corresponding to edges which are cut by the plane or isosurface (in the standard ordering discussed earlier in this chapter; see page 107). It is now easy to get the coordinates of the endpoints of the cut edges using the standard numbering embodied in the tables; we then linearly interpolate along the cut edges, based on the values on their endpoints, to obtain a list of coordinates of the intersections of the plane or isosurface with the cells. This list of points now needs to be ordered so that the polygons of intersection can be drawn properly.
We associate with each critical cell a pattern number between 0 and 255 (non-inclusive) which denotes in one number the pattern of its vertices where the function value is negative. The pattern number is arrived at by assigning the number 2k to the kth vertex in the cell, then adding together for each cell the numbers assigned to its vertices that have negative values. We now create a new pattern array which is ncells * ne long and in which the entry corresponding to each cut edge contains the same pattern number as its adjacent cell; i. e., if cell j has cut edge i and pattern number n, then pattern [i * ne + j] will contain n.
The _poly_permutations array. To each pattern, there corresponds a permutation of the edges so that they occur in the order in which the edges are to be connected. Let each such permutation be stored as a list of integers from 0 to ne - 1 such that sorting the integers into increasing order rearranges the edges at the corresponding indices into the correct order. (The position of unsliced edges in the list is arbitrary as long as the sliced edges are in the proper order relative to each other.) Let these permutations be stored in a ne-by-254 array _poly_permutations.
_poly_permutations is computed (one time only) as follows. When slice3.py is imported, _construct3 is called four times, once for each type of cell. _construct3 first creates a mask array below dimensioned (2nv - 2) by nv. The row below [k] has an entry for each vertex, marked 0 or 1 corresponding to the pattern number k + 1. _construct3 now calls find_mask (see 9.3.9 "Finding Edges Cut by Isosurfaces: find_mask") with parameters below and the _node_edges array for that particular type of cell. find_mask returns an array (called mask) (2nv - 1) by ne in size; each set of ne consecutive entries is filled with an edge mask, i. e., the entry corresponding to an edge in the standard order is 1 or 0 according as the corresponding edge is cut or not. _construct3 now calls construct3, a function in arrayfnsmodule (see 9.3.10 "Order Cut Edges of a cell: construct3"), with mask and the cell type as parameters.
The purpose of construct3 is to determine an order for the cut edges so that the polygons representing the plane or isosurface cut of the cell will be drawn properly. construct3 does this by calling an auxiliary function walk3 inside a loop, each call of walk3 being with the next ne entries of mask. walk3 not only decides the correct order of the points of intersection in order to draw the polygons, but also decides whether there are disjoint polygonal intersections with this cell. The walk3 algorithm begins with the lowest numbered cut edge (and marks that edge as having been used) and examines the lowest numbered face incident upon this edge. There must be at least one other cut edge on this face. If the face is triangular, it looks first at the next edge counterclockwise (in the outwards normal direction), then (if necessary) the next one clockwise. On a square face it looks first at the opposite edge, then at the next one clockwise, then counterclockwise. When it has selected an edge, it goes to the other face incident upon that edge and repeats the process. If at some point no unused edge can be found, then that means a closed polygon has been found. The next unused edge with the lowest number is chosen (if there is one) and the process repeats. In the latter case, there is more than one disjoint polygonal intersection with the cell, and the number ne * (no. of disjoint polygons so far) is added to the edge permutations.
Thus, for each cut cell in the mesh, _poly_permutations tells the order that the cutting points must be connected, and how many polygonal intersections there are with the cell. In the function slice3, the following instructions compute subscripts into the array of points in the correct order for drawing:
The order array is now used as a set of subscripts so that we can extract the coordinates of the cutting points in the proper order. Once this has been done, the array whose entries give the number of vertices in each polygon is calculated.
There remains only the question of splitting the points in a single cell into multiple disjoint polygons. To do this, recall that when computing _poly_permutations, we had added ne (the number of edges on this type of cell) to any second disjoint polygon's edge list, 2 * ne to any third one, etc. The following will now give an array whose entries corresponding to the edge orderings for each cell will be 0 for the first disjoint polygon, 1 for the second, 2 for the third, and 3 for the fourth (if there are that many).
Now pattern jumps by 4 between cells, smaller jumps within cells get the list of places where a new value begins, and form a new pattern with values that increment by 1 between each plateau. Then the following relatively straightforward computation computes the nverts array. In order to fully appreciate how the algorithm works, we have indicated the results supposing that we began with the pattern [0, 0, 0, 1, 1, 1, 1, 2,2,2,4,4,4,4,4,5,5,5,8,8,8].
