Warning: jsMath requires JavaScript to process the mathematics on this page.
If your browser supports JavaScript, be sure it is enabled.

Binomial Coefficient

From QED

< PlasmaWiki(Link to this page as [[PlasmaWiki/Binomial Coefficient]])

Jump to: navigation, search

The Binomial Coefficient

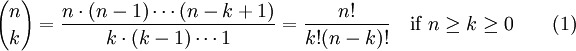${n \choose k} = \frac{n \cdot (n-1) \cdots (n-k+1)}{k \cdot (k-1) \cdots 1} = \frac{n!}{k!(n-k)!} \quad \mbox{if } n\geq k\geq 0 \qquad \mbox{(1)}$ </dd>

Read n 'choose' k, describes the number of ways to choose k elements from an n element set.

This may be extended to a more general definition which allows the upper index to be any complex number, and the lower index is any integer:

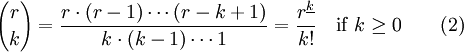${r \choose k} = \frac{r \cdot (r-1) \cdots (r-k+1)}{k \cdot (k-1) \cdots 1} = \frac{r^{\underline{k}}}{k!} \quad \mbox{if } k \geq 0 \qquad \mbox{(2)}$ </dd>

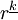Where $r^{\underline{k}}$ is the rising factorial power.

The following is a table of the most useful identities. Eventually, each will link to a proof thereof.

The 'top ten' binomial coefficent identities. (From Concrete Mathematics)
Identity	Constraints	Name
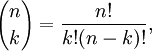
${n \choose k} = \frac{n!}{k! (n - k)!},$	integers 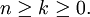$n \geq k \geq 0.$	Factorial Expansion
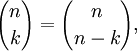
${n \choose k} = {n \choose n - k},$	integer $n \geq 0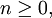,$ integer $k .$	Symmetry
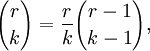
${r \choose k} = \frac{r}{k}{r - 1 \choose k - 1},$	integer 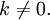$k \neq 0.$	Absorption/Extraction
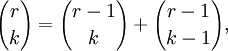
${r \choose k} = {r - 1 \choose k} + {r - 1 \choose k - 1},$	integer $k .$	Addition/Induction
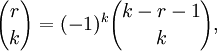
${r \choose k} = (-1)^k {k - r - 1 \choose k},$	integer $k .$	Upper Negation
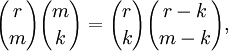
${r \choose m}{m \choose k} = {r \choose k} {r - k \choose m - k},$	integers $m, k .$	Trinomial Revision
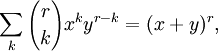
$\sum_k{r \choose k} x^k y^{r-k} = (x + y)^r,$	integer 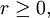$r \geq 0,$ or $\| x / y \| < 1.$	Binomial Theorem
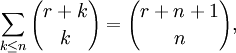
$\sum_{k \leq n}{r + k \choose k} = {r + n + 1 \choose n},$	integer $n .$	Parallel Summation
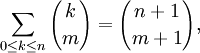
$\sum_{0 \leq k \leq n}{k \choose m} = {n + 1 \choose m + 1},$	integers 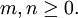$m,n \geq 0.$	Upper Summation
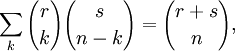
$\sum_k{r \choose k}{s \choose n - k} ={r + s \choose n},$	integer $n .$	Vandermonde Convolution