Warning: jsMath requires JavaScript to process the mathematics on this page.
If your browser supports JavaScript, be sure it is enabled.

Leibniz Integral Rule

From QED

< PlasmaWiki(Link to this page as [[PlasmaWiki/Leibniz Integral Rule]])

Jump to: navigation, search

The Leibniz Integral Rule gives a formula for the differentiation of a definite integral whose limits are the function of the differentiable variable.

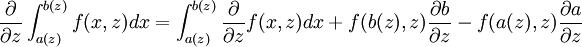
$\frac{\partial}{\partial z}\int_{a(z)}^{b(z)}{f(x,z) dx} = \int_{a(z)}^{b(z)}{\frac{\partial}{\partial z} f(x,z) dx} + f(b(z), z) \frac{\partial b}{\partial z} - f(a(z), z) \frac{\partial a}{\partial z}$

It's sometimes known as differentiation under the integral sign , and it was made famous as one of the favorite tricks of R.P. Feynman.

Mathworld gives an unusual definite integral which this can be used to evaluate:

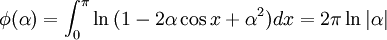
$\phi(\alpha) = \int_{0}^{\pi}{\ln{(1 - 2 \alpha \cos{x} + \alpha^2)} dx} = 2 \pi \ln{|{\alpha}|}$

for $| α | > 1$ (Derivation to follow).

It also gives useful identities for Gaussian integrals, as shown in Townsend (although this is a noncovering example, as it doesn't involve limits which are functions of the differentiating variable):

We take the standard Gaussian

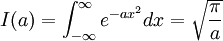
$I(a) = \int_{-\infty}^{\infty} e^{- a x^2} dx = \sqrt{\frac{\pi}{a}}$

And then note that

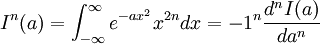
$I^{n}(a) = \int_{-\infty}^{\infty} e^{ - a x^2} x^{2 n} dx = -1^n \frac{d^n I(a)}{d a^n}$

Hence

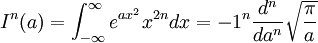
$I^{n}(a) = \int_{-\infty}^{\infty} e^{a x^2} x^{2 n} dx = -1^n \frac{d^n}{da^n} \sqrt{\frac{\pi}{a}}$

The real power lies where adding 'dummy' variables to the limits, and differentiating over these. Usually, the last two terms are not difficult to evaluate, while the derivative of the integrand with respect to z is in fact much easier to evaluate.

Due to the form of the rule, this technique is often useful when evaluating integral transforms.

None thus far.