MHD equations

From QED

< PlasmaWiki(Link to this page as [[PlasmaWiki/MHD equations]])
Jump to: navigation, search

There are nine single-fluid MHD equations (three scalar equations and two vector equations). These provide a fluid description of a one species plasma. They are derived in the limit of a quasi-neutral, collisionless plasma, neglecting electron inertia. They are:

Continuity equation :

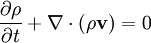
\frac{\partial\rho}{\partial t}+\nabla\cdot\left(\rho\mathbf{v}\right)=0

Momentum equation (d/dt is the Lagrangian derivative ):

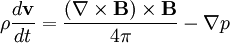
\rho\frac{d \mathbf{v}}{d t}=\frac{\left(\nabla\times\mathbf{B}\right)\times\mathbf{B}}{4\pi}-\nabla p

Energy equation (γ is the adiabatic constant 5/3, and d/dt is the Lagrangian derivative ):

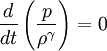
\frac{d}{dt}\left(\frac{p}{\rho^{\gamma}}\right)=0

Field equation (for ideal MHD, η = 0):

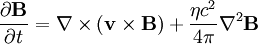
\frac{\partial\mathbf{B}}{\partial t}=\nabla\times\left(\mathbf{v}\times\mathbf{B}\right)+\frac{\eta c^{2}}{4\pi}\nabla^{2}\mathbf{B}

It is also necessary that there are no magnetic monopoles :

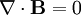
\nabla \cdot \mathbf{B}=0

These equations rely on the use of the following other equations:

Ohm's Law :

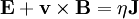
\mathbf{E}+\mathbf{v}\times\mathbf{B}=\eta \mathbf{J}

Faraday's Law :

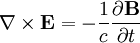
\nabla\times\mathbf{E}=-\frac{1}{c}\frac{\partial\mathbf{B}}{\partial t}

Ampere's Law (neglecting the displacement current):

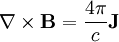
\nabla\times\mathbf{B}=\frac{4\pi}{c}\mathbf{J}

This page was recovered in October 2009 from the Plasmagicians page on MHD_equations dated 21:27, 10 April 2007.

Retrieved from "https://qed.princeton.edu/main/PlasmaWiki/MHD_equations"
Personal tools