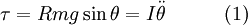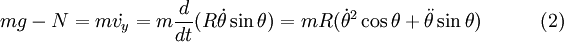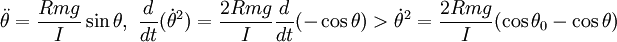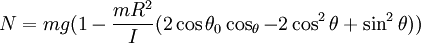CM J04 3

From QED

< PlasmaWiki | Prelims(Link to this page as [[PlasmaWiki/Prelims/CM J04 3]])
Jump to: navigation, search

A thin stick with some arbitrary linear mass density μ(x) along it is initially at rest. It has one end on a table and makes an angle θ0 with the vertical. The stick-table contact point has an infinite coefficient of friction.

Let m be the total mass of the stick, R be the distance from the contact point to the center of mass, ICM, and g be the acceleration due to gravity.

(a) The stick is released from rest and allowed to fall to the table. Find the condition that the end of the stick initially in contact with the table does rise from the table as the stick falls. Express the condition in terms of θ0,m,g,R, and ICM.
(b) Now consider a specific mass distribution. Let the mass be uniformly distributed along the length. For what what range of initial angles θ0 will the stick eventually lift off the table?
(c) Consider a specific mass distribution. The mass is concentrate in two points of equal mass, one at either end of the stick. Now for what range of initial angles θ0 will the stick eventually lift off the table?

What should the answer look like? Clearly, the scale of m and g are irrelevant (so long as they are positive). It should also be impossible for a distribution that is linearly symmetric about the center of mass to have the endpoint lift, so the answer to the last two parts should yield an empty range.

We suppose that the endpoint of the stick touching the ground is fixed. It is fixed in the horiztonal dimension by an infinite frictional force f. It is fixed in the vertical dimension by a normal force N. If ever N < 0, this point would actually lift from the ground.

Let's examine the equations of motion.

We get the moment of inertia from the from the parallel axis theorem:

I = mR2 + ICM

The torque is:

\tau = Rmg \sin \theta = I \ddot{\theta} \quad\quad\quad(1)

Finally, the force along the y axis is

mg - N = m \dot{v_y} = m {d \over dt}(R \dot{\theta} \sin \theta ) = mR (\dot{\theta}^2 \cos \theta + \ddot{\theta} \sin \theta ) \quad\quad\quad(2)

From (1),

\ddot \theta = {Rmg \over I } \sin \theta , ~{d \over dt } ( {\dot\theta}^2) = {2Rmg \over I } { d \over dt } (-\cos\theta) > {\dot\theta}^2 = {2Rmg \over I } (\cos\theta_0 - \cos \theta)

Plugging these results into (2) yields

N = mg ( 1 - {mR^2 \over I } (2 \cos\theta_0 \cos_\theta - 2\cos^2 \theta + \sin^2 \theta) )

Let h = 2cosθ0cosθ − 2cos2θ + sin2θ

N is minimized when h is maximized. When Nmin < 0, the end point rises from the table.

{ dh \over d\theta} = 2 \sin \theta (3 \cos \theta - \cos\theta_0 )


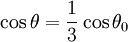When \cos\theta = {1 \over 3} \cos\theta_0, h is maximized.

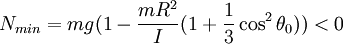
N_{min}= mg( 1 - {mR^2 \over I} (1 + {1 \over 3} \cos^2 \theta_0 )) < 0

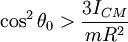
\cos^2\theta_0 > {3 I_{CM} \over mR^2}

In this case, 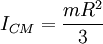I_{CM} = {mR^2 \over 3}.

cosθ0 > 1. This has no solutions, thus there is no such range.

In this case, ICM = mR2.

cos2θ0 > 3.

There is no range of θ0 which satisfies this inequality. Thus, we can say the stick never lifts off the table.

Solved by Jongsoo Yoo on OCT 15. -- Note (get a username!)

Pencil Prize Awarded on OCT 18: Image:PlasmaWiki Pencilprize.jpg

This page was recovered in October 2009 from the Plasmagicians page on Prelim_J04_Mech3 dated 14:53, 20 October 2006.

Retrieved from "https://qed.princeton.edu/main/PlasmaWiki/Prelims/CM_J04_3"
Personal tools