CM M05 2
From QED
Determine the equilibrium shape y(x) of the suspension cable in a bridge shown in the figure. The length of the roadbed is L and the mass M is so large that you can neglect the weight of the suspension cable and the verticle supporting cables. the lengths of the vertical cables are adjusted so that there is no shear stress on the roadway. You can also assume that the vertical cables are close enough that y can be approximated as an analytic function of x.
What should the answer look like? At first glance it appears that this is the standard catenary problem ( Prelim_J00_Mech1 ). However, there is a subtle but important difference -- here the weight is not distributed along 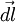 but dx. This changes the result, but it makes calculations much simpler.
but dx. This changes the result, but it makes calculations much simpler.
The tensile force is directed along the cable. The horizontal forces are balanced, so parameterize everything in terms of FH (since it is constant). The tensile force has magnitude 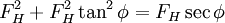 .
.
The vertical tensile force balances gravity (the span mass length density is 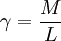 ). Working to first order
). Working to first order
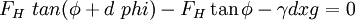
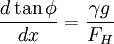
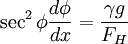
Pleasingly, 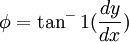 when dx > 0, and so
when dx > 0, and so
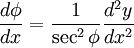
By the rule for the Differentiation of Inverse Functions . Thus
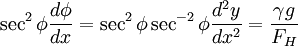
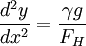
Yes indeed, suspension cables are more closely parabolic than catenaries.
The equation for y gives
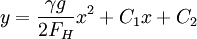
Let he towers be placed at x = xtower and x = − xtower, leaving the origin for the center of the parabola.
Let the height of the towers be 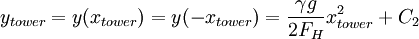 (where C1 is eliminated by symmetry).
(where C1 is eliminated by symmetry).
Then 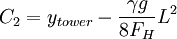 , where L is the length of the span.
, where L is the length of the span.
We check to see if FH is specified by this system by equating forces. Twice the vertical force applied at one of the endpoints is equal to gravitational force on the span, Mg.
The angle at the towers is 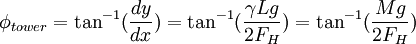 .
.
The horizontal and vertical forces are then FH = Ftotcosφtower and 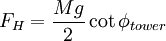 .
.
By the formula 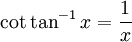
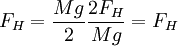
So we discover that FH is not specified, any number may be chosen to achieve the desired shape (well, so long as it leads to a cable that's higher than the roadbed).
So, finally, for any reasonable choice of FH,
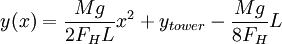
This page was recovered in October 2009 from the Plasmagicians page on Prelim_M05_Mech2 dated 05:38, 21 November 2006.












