Warning: jsMath requires JavaScript to process the mathematics on this page.
If your browser supports JavaScript, be sure it is enabled.

EM J04 1

From QED

< PlasmaWiki | Prelims(Link to this page as [[PlasmaWiki/Prelims/EM J04 1]])

Jump to: navigation, search

Consider a long cylindrical capacitor, which consists of two metallic concentric cylinders of length l. The radii of the cylinders are a (outer) and b (inner), 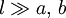$l\gg a,\, b$ . The axes of the two cylinders coincides with z-axis. As an added bonus the cylinders are free to rotate about the z-axis independently from each other and without friction. The voltage between the two conductors is U. 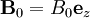Originally, at time t=0 there is also magnetic field $\mathbf{B}_{0}=B_{0}\mathbf{e}_{z}$ in z-direction.

a. Determine charges on each of the cylinders at t=0 and the electric field 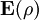$\mathbf{E}(\rho)$ . (magnitude and direction), in the volume between teh cylinders as functions of the distance $ρ$ from the axis. As in all parts of this exam, either MKSA or Gaussian units may be employed.

b. The magnetic field is slowly reduced, remaining parallel to the z-axis, until it vanishes at some moment of time, $t 0$ . This causes the two cylinders to start rotating. Use Faraday's law to determine the angular momenta, 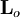$\mathbf{L}_{o}$ of each of them after the magnetic field was reduced to zero. You may ignore the magnetic field produced by the rotation of the conductors. Also ignore any fringing of the fields at the ends of the cylinders.

c. Recall that the electromagnetic fields contain a momentum density, 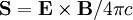$\mathbf{S}=\mathbf{E}\times\mathbf{B}/4\pi c$ (Gaussian units). Taking this fact into account evaluate the angular momentum (magnitude and direction) contained in the electromagnetic field in teh initial configuration. Compare it with the total angular momentum of the capacitor in the final configuration.

d. How will the result for the angular momentum of the two cylinders change (increase, decrease or remain the same) if the magnetic field of the rotating cylinders were taken into account?

Solution 1

Solution 2

We use a gaussian integral around the inner cylinder:

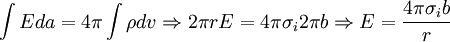
$\int Eda=4\pi\int\rho dv\Rightarrow2\pi rE=4\pi\sigma_{i}2\pi b\Rightarrow E=\frac{4\pi\sigma_{i}b}{r}$

The potential difference is given by:

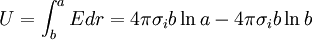
$U=\int_{b}^{a}Edr=4\pi\sigma_{i}b\ln a-4\pi\sigma_{i}b\ln b$

Solving for $σ i$ :

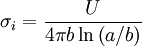
$\sigma_{i}=\frac{U}{4\pi b\ln\left(a/b\right)}$

The potential is given by:

Φ = 4πσ i b ln r

So that the charge on the outer cylinder is given by:

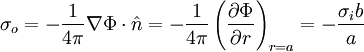
$\sigma_{o}=-\frac{1}{4\pi}\nabla\Phi\cdot\hat{n}=-\frac{1}{4\pi}\left(\frac{\partial\Phi}{\partial r}\right)_{r=a}=-\frac{\sigma_{i}b}{a}$

We can integrate the charge densities to get the total charge:

<math>Q_{i}=2\pi bl\sigma_{i}=l\frac{U}{2\ln\left(a/b\right)}</math>

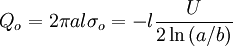
$Q_{o}=2\pi al\sigma_{o}=-l\frac{U}{2\ln\left(a/b\right)}$

And the electric field is given by:

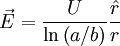
$\vec{E}=\frac{U}{\ln\left(a/b\right)}\frac{\hat{r}}{r}$

The Faraday's Law gives:

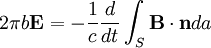
$2\pi b\mathbf{E}=-\frac{1}{c}\frac{d}{dt}\int_{S}\mathbf{B}\cdot\mathbf{n}da$

So that for the inner cylinder:

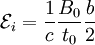
$\mathcal{E}_{i}=\frac{1}{c}\frac{B_{0}}{t_{0}}\frac{b}{2}$

The torque will be:

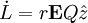
$\dot{L}=r\mathbf{E}Q\hat{z}$

So that the induced angular momentum will be:

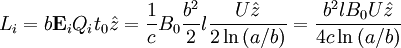
$L_{i}=b\mathbf{E}_{i}Q_{i}t_{0}\hat{z}=\frac{1}{c}B_{0}\frac{b^{2}}{2} l\frac{U\hat{z}}{2\ln\left(a/b\right)}=\frac{b^{2}lB_{0}U\hat{z}}{4c\ln\left(a/b\right)}$

For the outer cylinder:

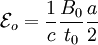
$\mathcal{E}_{o}=\frac{1}{c}\frac{B_{0}}{t_{0}}\frac{a}{2}$

So that:

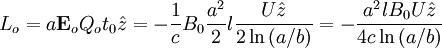
$L_{o}=a\mathbf{E}_{o}Q_{o}t_{0}\hat{z}=-\frac{1}{c}B_{0}\frac{a^{2}}{2} l\frac{U\hat{z}}{2\ln\left(a/b\right)}=-\frac{a^{2}lB_{0}U\hat{z}}{4c\ln\left(a/b\right)}$

And the total angular momentum is:

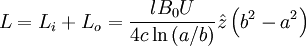
$L=L_{i}+L_{o}=\frac{lB_{0}U}{4c\ln\left(a/b\right)}\hat{z}\left(b^{2}-a^{2}\right)$

The field momentum is given by the Poynting Vector:

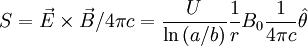
$S=\vec{E}\times\vec{B}/4\pi c=\frac{U}{\ln\left(a/b\right)}\frac{1}{r}B_{0}\frac{1}{4\pi c}\hat{\theta}$

So that its angular momentum is:

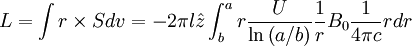
$L=\int r\times Sdv=-2\pi l\hat{z}\int_{b}^{a}r\frac{U}{\ln\left(a/b\right)}\frac{1}{r}B_{0}\frac{1}{4\pi c}rdr$

where the integral over z and $θ$ is already done. Integrating over r:

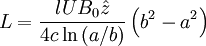
$L=\frac{lUB_{0}\hat{z}}{4c\ln\left(a/b\right)}\left(b^{2}-a^{2}\right)$

The momentum would decrease, as the cylinders turn to oppose the change in $\vec{B}$ in the same direction as before. This field would have angular momentum in the same direction, so that the cylinders themselves would have less angular momentum.