EM M97 2
From QED
Solution 1
PlasmaWiki_Prelims_EM_M97_2.pdf (help · info)
Solution 2
An infinite conducting plane (taken here to be the x-y
plane) is electrically neutral and carries a uniform
surface current 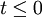 and K = K0 for t>0 with K0
equal to a constant.
and K = K0 for t>0 with K0
equal to a constant.
a. Find the magnitude and direction of the electric and magnetic fields a height z above the plane.
b. Compute the total power radiated per unit area of the x-y plane
The magnetic field is given by:
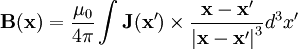
We have 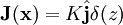 so taking the cross product and the integral
over z :
so taking the cross product and the integral
over z :
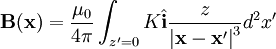
Performing this integral:
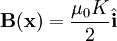
However, this can obviously only travel at the speed of light, so that:
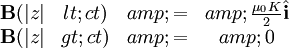
Which gives us an electric field by Faraday's Law:
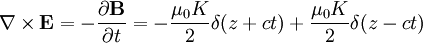
If we think of this as electromagnetic radiation, we wouldn't have E parallel to the direction of travel, and it must be perpendicular to B. Therefore, if we write:
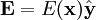
We find:
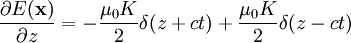
So that:
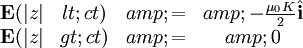
We find the power:
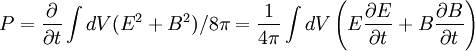
Per unit area, using symmetry:
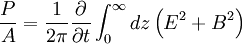
Plugging in, using Θ(s) as the heavyside function:
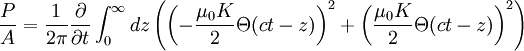
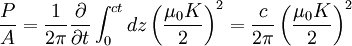
The power radiated per unit area, as defined on page 347 of Griffiths, is simply the Poynting vector (Given in SI units, with |E| = c |B|):
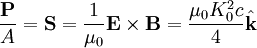
This page was recovered in October 2009 from the Plasmagicians page on Prelim_M97_EM2 dated 17:34, 20 December 2006.












