QM J00 2

From QED

< PlasmaWiki | Prelims(Link to this page as [[PlasmaWiki/Prelims/QM J00 2]])
Jump to: navigation, search

First Solution

PlasmaWiki_Prelims_QM_J00_2.pdf (help ยท info)

Second Solution

Two interacting particles have Hamiltonian 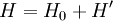H=H_{0}+H^{\prime}, where:

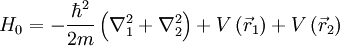
H_{0}=-\frac{\hbar^{2}}{2m}\left(\nabla_{1}^{2}+\nabla_{2}^{2}\right)+V\left(\vec{r}_{1}\right)+V\left(\vec{r}_{2}\right)

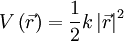
V\left(\vec{r}\right)=\frac{1}{2}k\left|\vec{r}\right|^{2}

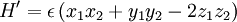
H^{\prime}=\epsilon\left(x_{1}x_{2}+y_{1}y_{2}-2z_{1}z_{2}\right)

Let us define ω such that k = mω2. The second order energy correction for a non-degenerate state is given by:

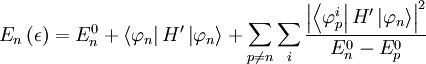
E_{n}\left(\epsilon\right)=E_{n}^{0}+\left\langle \varphi_{n}\right|H^{\prime}\left|\varphi_{n}\right\rangle +\sum_{p\neq n}\sum_{i}\frac{\left|\left\langle \varphi_{p}^{i}\right|H^{\prime}\left|\varphi_{n}\right\rangle \right|^{2}}{E_{n}^{0}-E_{p}^{0}}

We also know that:

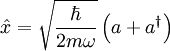
\hat{x}=\sqrt{\frac{\hbar}{2m\omega}}\left(a+a^{\dagger}\right)

We can define the eigenstates of the hamiltionian H0 as 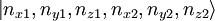\left|n_{x1},n_{y1},n_{z1},n_{x2},n_{y2},n_{z2}\right\rangle. The creation and annihilation operators act like:

Failed to parse (syntax error): a\left|\varphi_{n}\right\rangle =\sqrt{n}\left|\varphi_{n-1}\right\rangle&nbsp;;\qquad a^{\dagger}\left|\varphi_{n}\right\rangle =\sqrt{n+1}\left|\varphi_{n+1}\right\rangle


We find that since the operators x1 and x2 commute (and similarly for the y 's and z 's) and change the ket by one, the second term (first order correction) is zero. For the second order term, since we are in the ground state, we find nonzero contributions:

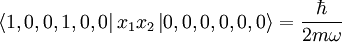
\left\langle 1,0,0,1,0,0\right|x_{1}x_{2}\left|0,0,0,0,0,0\right\rangle =\frac{\hbar}{2m\omega}

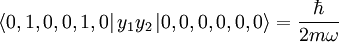
\left\langle 0,1,0,0,1,0\right|y_{1}y_{2}\left|0,0,0,0,0,0\right\rangle =\frac{\hbar}{2m\omega}

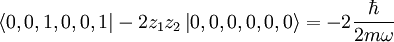
\left\langle 0,0,1,0,0,1\right|-2z_{1}z_{2}\left|0,0,0,0,0,0\right\rangle =-2\frac{\hbar}{2m\omega}

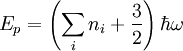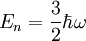We get the energy of the excited states to be E_{p}=\left(\sum_{i}n_{i}+\frac{3}{2}\right)\hbar\omega . The ground state is obviously then at E_{n}=\frac{3}{2}\hbar\omega. Inserting these into our equation for the energy shift, we get:

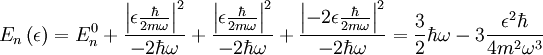
E_{n}\left(\epsilon\right)=E_{n}^{0}+\frac{\left|\epsilon\frac{\hbar}{2m\omega}\right|^{2}}{-2\hbar\omega}+\frac{\left|\epsilon\frac{\hbar}{2m\omega}\right|^{2}}{-2\hbar\omega}+\frac{\left|-2\epsilon\frac{\hbar}{2m\omega}\right|^{2}}{-2\hbar\omega}=\frac{3}{2}\hbar\omega-3\frac{\epsilon^{2}\hbar}{4m^{2}\omega^{3}}

Since there is no ω in the problem, we convert back to k: 

<math>E_{n}\left(\epsilon\right)=\frac{3}{2}\hbar\omega-3\frac{\epsilon^{2}\hbar\omega}{4k^{2}}=\left(\frac{3}{2}-3\frac{\epsilon^{2}}{4k^{2}}\right)\hbar\sqrt{\frac{k}{m}}</math>

This page was recovered in October 2009 from the Plasmagicians page on Prelim_J00_QM2 dated 04:59, 23 December 2005.

Retrieved from "https://qed.princeton.edu/main/PlasmaWiki/Prelims/QM_J00_2"
Personal tools